상관계수 Correlation 이란 무엇인가??? [빅공남! 통계 같이 공부해요]

상관계수 Correlation 이란 무엇인가?는 통계, 기초통계학, 빅데이터, 머신러닝 등에서 반드시 알아야할 기초 개념중에 하나입니다. 상관계수를 공부하려면 먼저 공분산의 개념을 이해해야기 때문에 지난 포스팅 빅공남 #12에서는 공분산을 주제로 영상을 만들었습니다. 오늘 포스팅을 위해 지난 포스팅 링크 먼저 추가하겠습니다.
공분산 Covariance 란 무엇인가??? [빅공남! 통계 같이 공부해요]
공분산(Covariance)란 무엇인가?는 통계 및 기초통계학 공부를 하는데 있어서 중요한 개념중에 하나 입니다. 빅데이터 분석기사 2과목 빅데이터 탐색에서 중요한 주제인 상관계수를 공부하기 앞서
seeyapangpang.tistory.com
상관계수(Correlation)은 결국 회귀분석(Regression)으로 가기 위한 과정이라고 보면 됩니다. 상관계수는 두 변수간의 직선형태의 모양의 분포를 어떻게 측정할 것일가?에 관한 주제라고 보시면 됩니다. 지난 포스팅에서 보듯이 먼저 공분산 식을 다시 한번 살펴보겠습니다.

공분산의 개념은 증가/증가 하는 경향 또는 감소/감소를 측정하는 개념으로 볼 수 있습니다.

그러면 공분산을 각각의 표준편차로 나눠서 계산한 상관계수는 어떤 의미를 가지는지 자세히 정리해보고자 합니다.
1. 상관계수(Correlation)?

상관계수(Correlation)은 위키피디아 그림에서 처럼 두 변수 X,Y의 관계가 얼마나 직선(Linear)에 가까운지에 대해서 나타내는 수치 입니다. 상관계수는 -1과1사이의 값을 가지고 1에 가까울수록 분포가 직선에 가까운 모양이 나오게 됩니다. 상관계수의 특징을 다음과 같이 정리해보았습니다.
[상관계수 특징]
1) 두 변수 X,Y 간에 공분산(Covariance)를 각각의 표준편차로 나눈 수치
2) -1에서 1사이의 값을 가짐.
3) 상관계수 = 0 의 의미 ☞ 직선 관계가 없다
4) +1이면 증가직선, -1이면 감소직선에 가까운 모양.
2. 상관계수(Correlation)의 부호 (+/-)
상관계수의 특징을 살펴보면 부호가 등장을 합니다. 이 부호는 공분산(증가/증가, 감소/감소)에서 나오는 부호가 됩니다. 양의 상관관계(+), 음의 상관관계(-)라고 합니다. 아래 그림을 보면서 이해하면 이해가 쉽게 갈 수 있습니다.
[상관계수의 부호]
1) Positive Correlation : 증가 직선형태에 분포
2) Negative Correlation : 감소 직선형태에 분포
3. Strong/Weak Correlation??
상관계수가 강하다(Strong)/약하다(Weak)하다의 개념은 상관계수가 +1 또는 -1 숫자에 가까워 질 때를 의미합니다. 얼마나 직선에 붙어있는지에 관한 내용입니다.
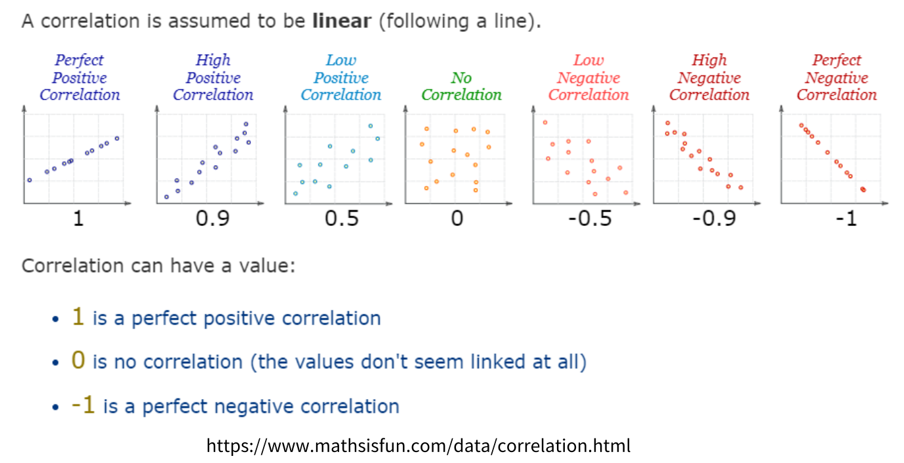
1) Perfect Positive Correlation : 완전 증가직선
2) Perfect Negative Correlation : 완전감소직선
3) Positive Correlation : 증가 직선에 가까운 분포
☞+1에 가까울수록 증가직선에 붙어 있음.
4) Negative Correlation : 감소 직선에 가까운 분포
☞-1에 가까울수록 감소직선에 붙어 있음.
4. 상관계수와 직선의 기울기???
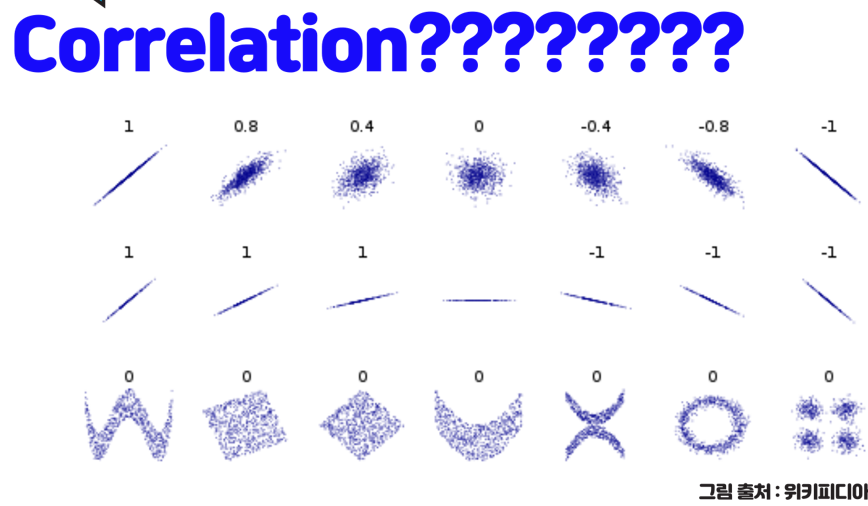
상관계수와 직선의 기울기와는 상관이 없습니다. 강하다/약하다는 직선 형태인가?에 관한 통계적 수치이고 직선의 기울기랑은 상관이 없습니다. 아래 위키피디아 그림의 2번째 행 그림을 보면 다시 확인할 수 있습니다.
5. 상관계수 다음 주제는? ☞ 회귀분석
상관계수(Corrleation)의 개념을 살펴보면 결국 두변수 X,Y간의 직선관계가 있는지 측정하는 통계량임을 알 수 있습니다. 다음 주제는 그 직선을 어떻게 찾을 것인가?가 중요한 이슈가 될 것입니다. 직선을 찾아가는 과정이 회귀분석(Regression)이 될 예정이고 추후에 포스팅하도록하겠습니다.
수학을 전공한 빅데이터를 공부하는 남자 빅공남은 추후 선형대수와 관련해서 쉽게 이해할 수 있는 내용을 정리해보고자 합니다. 오늘 긴 포스팅은 여기서 마치겠습니다.
[빅공남 유트브 채널 바로가기]
[빅공남! 통계 같이해요 바로가기]
[빅공남! 문과생을 위한 고등수학 13강]
| 다중 선형 회귀분석 Multiple Linear Regression 이란 무엇인가??? [빅공남! 통계 같이 공부해요] (0) | 2021.12.31 |
|---|---|
| 선형 회귀분석 기초 쌓기 Linear Regression 이란 무엇인가??? [빅공남! 통계 같이 공부해요] (0) | 2021.12.31 |
| 공분산 Covariance 란 무엇인가??? [빅공남! 통계 같이 공부해요] (3) | 2021.12.31 |
| 변수선택(필터/랩퍼/임베디드) [빅공남! 통계 같이 공부해요] (0) | 2021.12.31 |
| 변수 Feature vs Target, Feature Engineering [빅공남! 통계 같이 공부해요] (0) | 2021.12.30 |








댓글