선형 회귀분석 기초 쌓기 Linear Regression 이란 무엇인가??? [빅공남! 통계 같이 공부해요]

회귀분석(Regression) 이란 무엇인가?는 통계, 기초통계학, 빅데이터, 머신러닝 등에서 반드시 알아야할 기초 개념중에 하나입니다. 회귀분석(Regression)를 공부하려면 먼저 상관계수의 개념을 이해해야기 때문에 지난 포스팅 빅공남 13번 포스팅에서는 상관계수를 주제로 영상을 만들었습니다. 오늘 포스팅을 위해 지난 포스팅 링크 먼저 추가하겠습니다. 유튜브 영상은 포스팅 맨 아래에 있습니다.
빅데이터 분석기사 2과목 빅데이터 탐색에서 차원에 관한 주제를 공부하기 전에 회귀분석(Regression)을 공부하고 다루면 좋겠다는 생각이 들어서 내용을 준비하게 되었습니다. 지난 포스팅에서 처럼 상관계수가 +1, -1에 가까울 수록 직선에 가까워지는데 오늘은 그 직선을 찾는다는 것이 어떤 의미가 있는지에 관한 주제를 다뤄보고자 합니다.

1. 회귀분석 (중학교 수학 vs 기초통계??)

중학교 수학에서에서 1차 함수에서는 직선 그래프의 식을 배우게 됩니다. y=ax+b에서 a는 기울기, b는 y절편을 구하는 문제를 많이들 풀어 보셨을 것입니다. 두점 A(1,1), B(2,3)을 지나는 직선의 식은 y=2x-1의 식이됩니다. 여기서 중요한 부분은 이 직선의 식을 알고 있다는 것은 다른 x에 대해서 y를 알아낼 수 있다는 것입니다. 즉, x=3을 대입하면 y = 2*3-1 = 5가 나오는 것을 알 수 있습니다. 회귀분석은 직선의 경향을 나타내는 데이터를 가지고 최적화된 직선의 식을 찾고 결과를 예측하는 과정으로 볼 수 있습니다. 그래서 어떻게 보면 중학교 수학에서 좀더 확장된 개념이라고 생각을 하면 쉽게 이해할 수 있다고 생각이 들어서 위의 그림을 준비했습니다.

2. 회귀분석 and Feature(원인), Target(결과)
데이터 싸이언스에서 회귀분석을 공부해야 하는 이유는 결국 원인과 결과를 예측하는 하나의 방법으로도 볼 수 있기 떄문입니다. 그래서 먼저 원인, 결과에 해당하는 개념인 독립변수, 종속변수 개념을 다시 그림으로 리뷰해보도록 합니다.

초등학교 다닐때 한번쯤은 보았던 함수그림에서 보면 x에 따라서 y가 변하게 됩니다. 회귀분석은 결국 관측된 데이터로 부터 결과를 얻어내는 과정이라고 볼 수 있습니다.
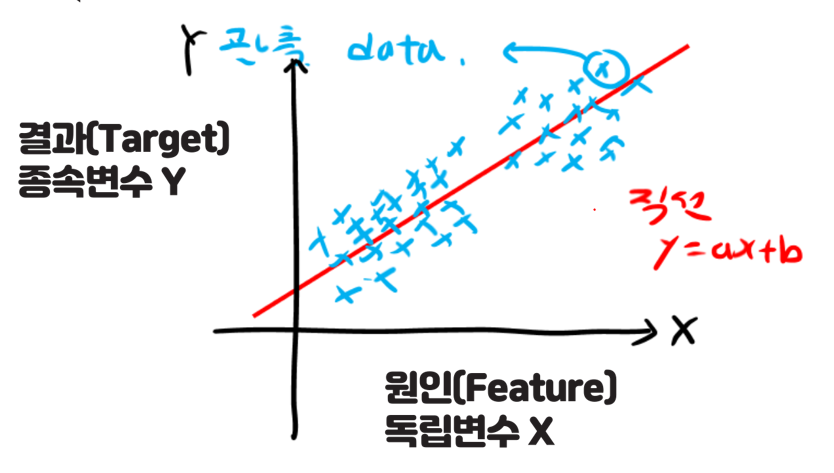
3. 선형 회귀분석이란?
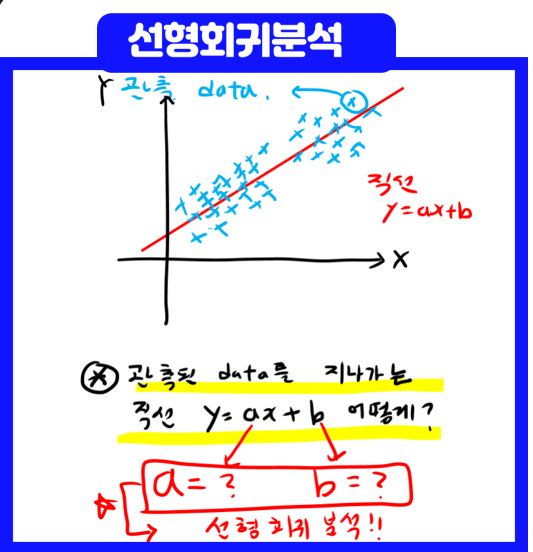
1) 관측된 Data를 좌표 (x,y)로 나타냄.
2) 여기서 관측된 Data (x,y)는
x 독립변수 : Feature(원인)
y 종속변수 : Target(결과)
3) 직선 y = ax+b를 만족하는 a,b를 찾아서 식을 만듦.
☞회귀분석
4) y= ax+b의 식을 알면, 임의의 원인변수 x로부터
결과 y 예측 가능
5) 회귀분석에서 나오는 가정??
3과목에서 다룰 예정...
(선형성, 독립성, 동분산성, 정규성)
3. 선형 회귀분석와 빅데이터 모델링?
그림과 같이 두 변수 x,y가 선형 관계에 있다고 생각해본다면, 회귀분석에서는 데이터들과 유사한 직선을 찾아내게 됩니다.
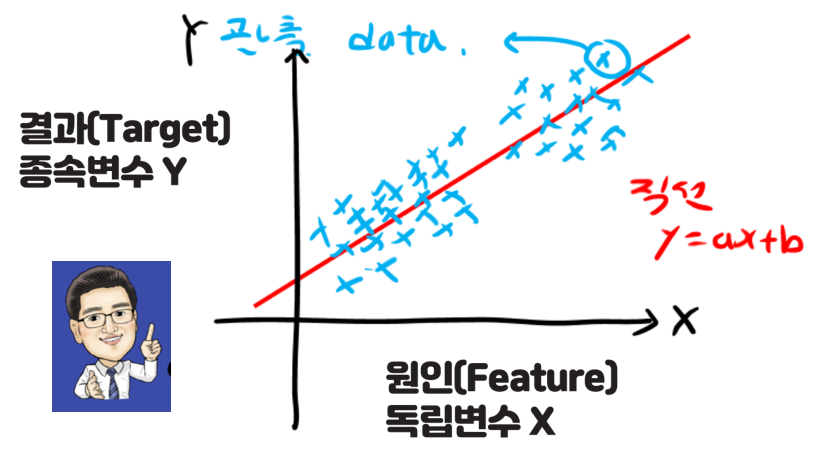
관측된 Data로부터 직선 y= ax+b를 알고 있는 상태에서 중요한 포인트는 결과를 추측할 수 있다는 점에서 빅데이터 모델링에 아주 중요한 개념이 될 수 있습니다. 데이터 분석을 한다는 것 자체가 관측된 Data Set으로 부터 예측을 하는 것을 의미하기에 회귀분석도 하나의 방법 또는 중요한 개념이 되는 것입니다. 아래 그림을 보면 결과를 예측한다는 의미를 좀더 직관적으로 이해할 수 있습니다.
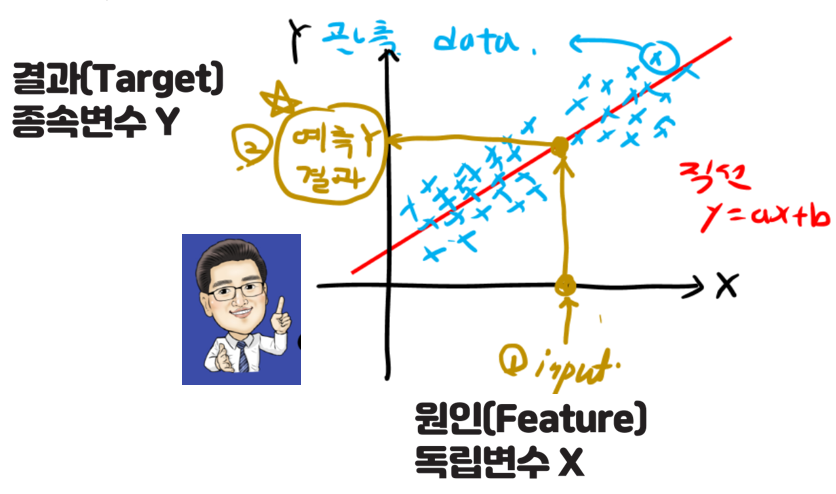
위의 그림처럼 임의의 한 변수 x가 관측된다면, y를 직선의 있는 결과로 대체에서 예측해볼 수 있습니다. 하지만 실제 관측 결과와는 당연히 차이가 있을 수 있습니다. 그래서 여기서 어떻게 해야 최적화된 직선을 찾을 수 있을까?에 대한 고민을 가지게 됩니다.
4. 회귀분석, 잔차, 최소제곱(최소자승)법?
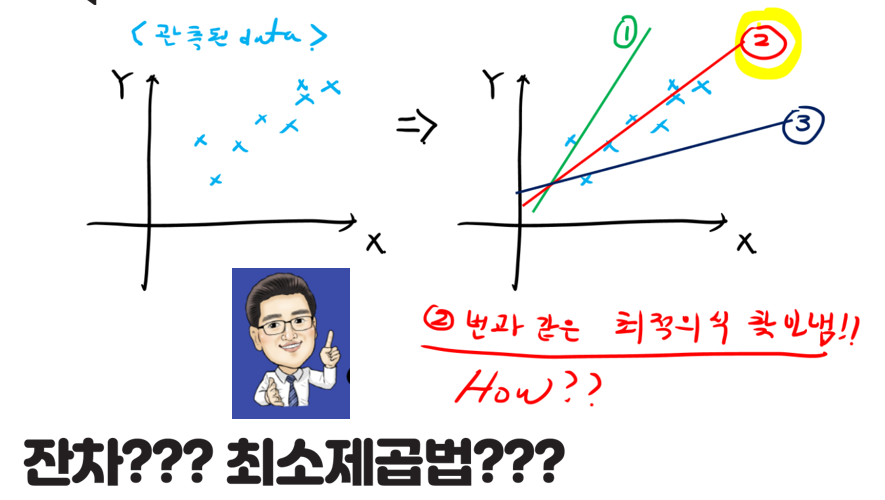
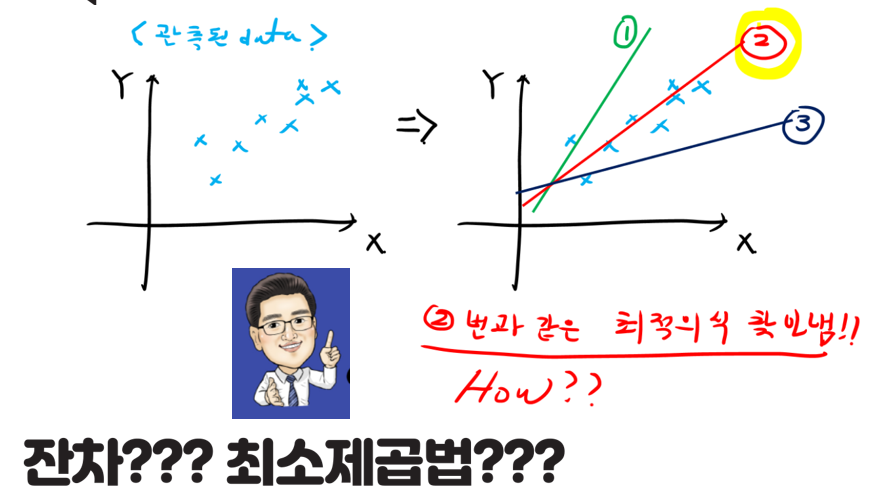
회귀분석에서 결국 최적화된 직선을 어떻게 찾아야 하기 위해선 어떤 방법으로 구할까?라는 고민에서 잔차라는 개념과 최소제곱(최소자승)법에 대해서 이해를 해야합니다. 먼저 2가지 개념을 잡고 아래 그림을 보겠습니다.
1) 잔차(Residual) : 관측된 Data와 직선과의 거리(차)
2) 최소자승법(List Squre Method)
잔차의제곱의 합이 최소가 되는 직선을 구함.
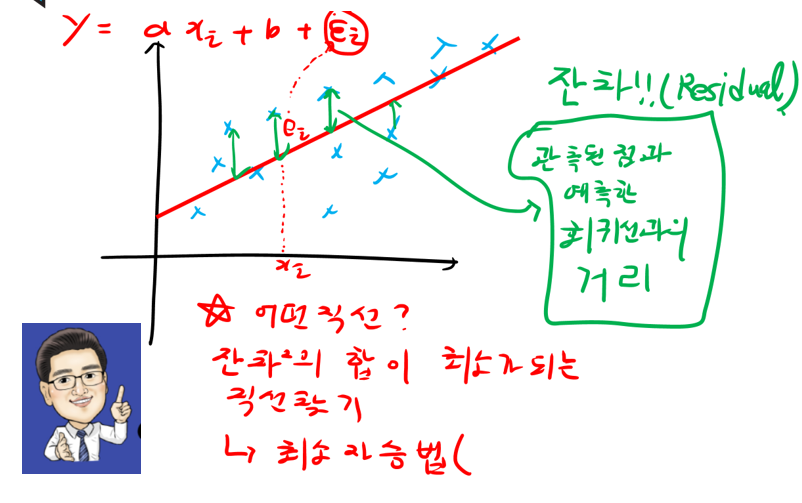
그림처럼 관측된 Data와 직선사이의 거리를 잔차라고 하며 이 값들은 직선보다 위이면 양수(+), 아래라면 음수(-)의 값들을 가지게 됩니다. 제곱의 합을 하면 이값들은 모두 양수가 될 수 있습니다. 이제 아래 그림을 보면서 잔차의 합이 작아지는 방향으로 직선을 찾아야 겠다는 생각이 들 수 있습니다. 즉 다시 한번 이 그림을 보면 2번 직선이 되야한다고 생각해 볼 수 있습니다.
회귀분석은 빅데이터, AI, 머신러닝 뿐만아니라 통계, 마케팅, 수학, 공학 등 다양한 분야해서 사용되는 중요한 개념입니다. 물론 회귀분석은 더욱 깊이 많은 내용을 공부해야하지만 오늘은 회귀분석의 기초를 쌓는다는 생각으로 열심히 준비했습니다. 차원을 이해하기 위해서는 행렬과 관련된 선형대수학을 이해해야하고 최소한 회귀분석의 개념을 대략 이해하고 차원 축소로 넘어가면 좋겠다는 생각을 하게 되었습니다. 오늘 포스팅은 이상 마무리 하겠습니다. 감사합니다 ^^
수학을 전공한 빅데이터를 공부하는 남자 빅공남은 추후 선형대수와 관련해서 쉽게 이해할 수 있는 내용을 정리해보고자 합니다. 오늘 긴 포스팅은 여기서 마치겠습니다.
| 다중공선성 MultiCollinearity 이란 무엇인가??? [빅공남! 통계 같이 공부해요] (0) | 2021.12.31 |
|---|---|
| 다중 선형 회귀분석 Multiple Linear Regression 이란 무엇인가??? [빅공남! 통계 같이 공부해요] (0) | 2021.12.31 |
| 상관계수 Correlation 이란 무엇인가??? [빅공남! 통계 같이 공부해요] (0) | 2021.12.31 |
| 공분산 Covariance 란 무엇인가??? [빅공남! 통계 같이 공부해요] (3) | 2021.12.31 |
| 변수선택(필터/랩퍼/임베디드) [빅공남! 통계 같이 공부해요] (0) | 2021.12.31 |







댓글