공분산 Covariance 란 무엇인가??? [빅공남! 통계 같이 공부해요]

공분산(Covariance)란 무엇인가?는 통계 및 기초통계학 공부를 하는데 있어서 중요한 개념중에 하나 입니다. 빅데이터 분석기사 2과목 빅데이터 탐색에서 중요한 주제인 상관계수를 공부하기 앞서 공분산 Covariance의 개념에 대해서 정리하는 포스팅을 준비했습니다.

상관계수를 공부하다보면 공분산(covariance)라는 말이 나옵니다. 상관계수는 그리고 두 변수간의 직선관계, 1차식의 계수를 찾아가는 과정이라고 하는데요... 하지만 다음과 같이 수식을 보면 머리가 아파집니다.

상관계수는 -1에서 1사이의 값을 가지고 직선성을 나타낸다고 하는데... 수식을 살펴보면 상관계수 식에는 공분산(Covariance) 개념이 들어갑니다. 수식을 파고들기보다는 직관적으로 어떤 의미를 가지는가?에 대해서 포커스를 마추고 오늘 포스팅을 준비했습니다.
1. 상관계수(Correalation)??
상관계수는 두 변수간의 직선관계를 나타내는 지표라고 보시면 됩니다. 두변수 X,Y가 같이 증가하거나 같이 감소하면서 직선의 모양을 나타낼때 통계적 수치량으로 분포의 모양을 대략적으로 유추할 수 있는 지표입니다. 위키피디아에 상관계수를 찾아보면 다음과 같이 그림을 볼 수 있습니다.

상관계수는 1이면은 증가하는 직선의 모양 분포, -1이면 감소하는 직선의 모양을 뜁니다. 그런데 상관계수 수식을 보면서 위의 직선관계가 이해가 잘 가지 않습니다. 다시 한번 수식을 살펴봅니다.

상관계수의 정의에 공분산 Covariance 즉, Cov(X,Y)가 등장합니다. 그러면 어떻게 직관적으로 증가, 감소형태의 직선 지표라는 것을 이해할 수 있을까요?
2. 공분산(Covariance) 직관적인 개념잡기
Step1) 공분산은 먼저 X좌표, Y좌표의 평균을 구하는데서 출발합니다.

공분산이란 위의 식처럼 각 점들을 X축, Y축에 x좌표, y좌표 점을 찍어서 평균을 구해봅니다.
Step2) X평균과 Y평균으로 4가지 영역 쪼개기
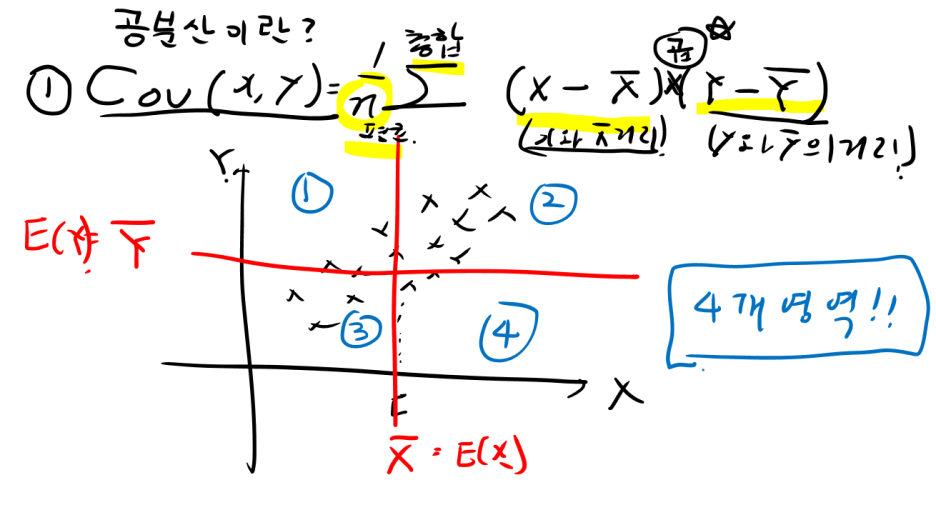
위의 그림처럼 X의 평균과 Y의 평균으로 영역을 나누게 되면 4가지 영역으로 분포를 분류할 수 있습니다.
Step3) 수식에서 (X-x평균)개념 이해하기
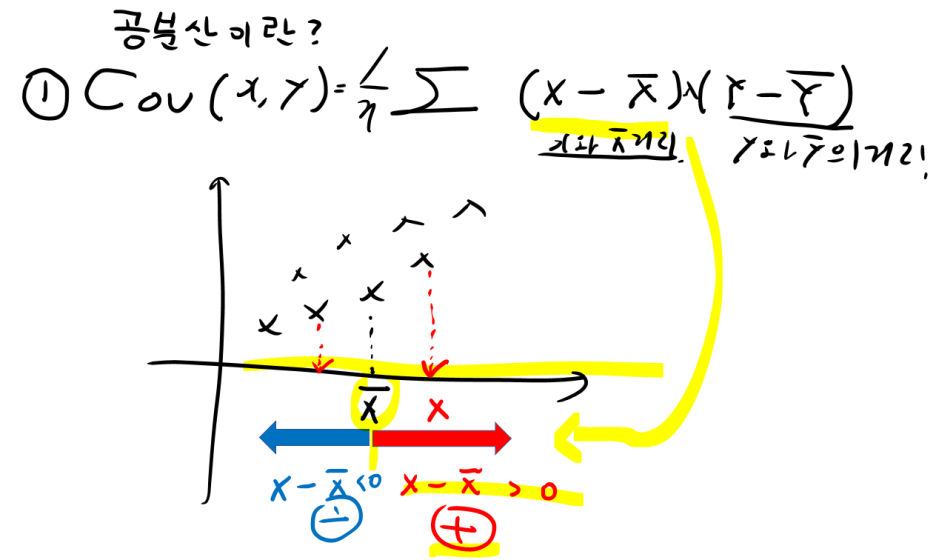
다음 그림과 같이 공분산 식에서 (X-x평균) 의 부호를 생각해볼 수 있습니다.
1) x평균보다 오른쪽 : 양수(+)
2) y평균보다 왼쪽 : 음수(-)
step4) 수식에서 (Y-y평균) 개념이해하기
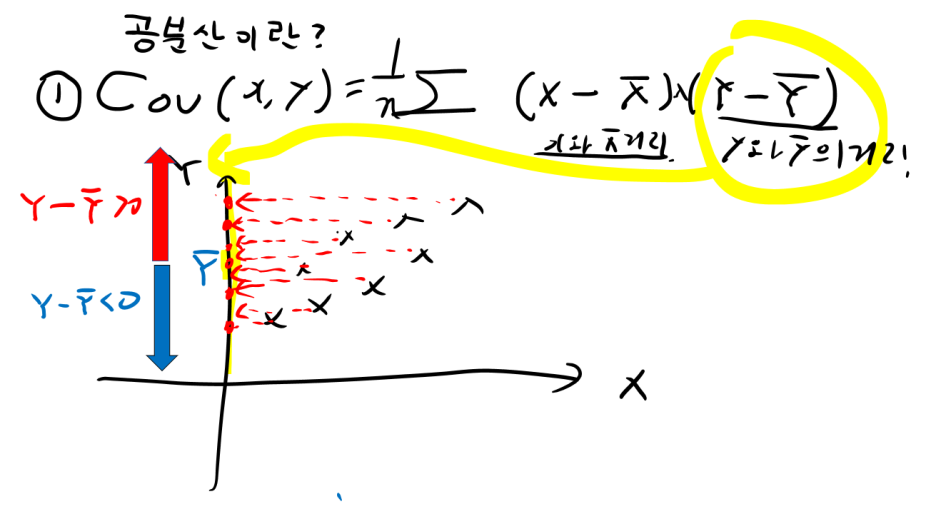
다음 그림과 같이 공분산 식에서 (Y-y평균) 의 부호를 생각해볼 수 있습니다.
1) y평균보다 위쪽 : 양수(+)
2) y평균보다 아래쪽 : 음수(-)
Step5) 수식에서 4가지 영역의 부호판정
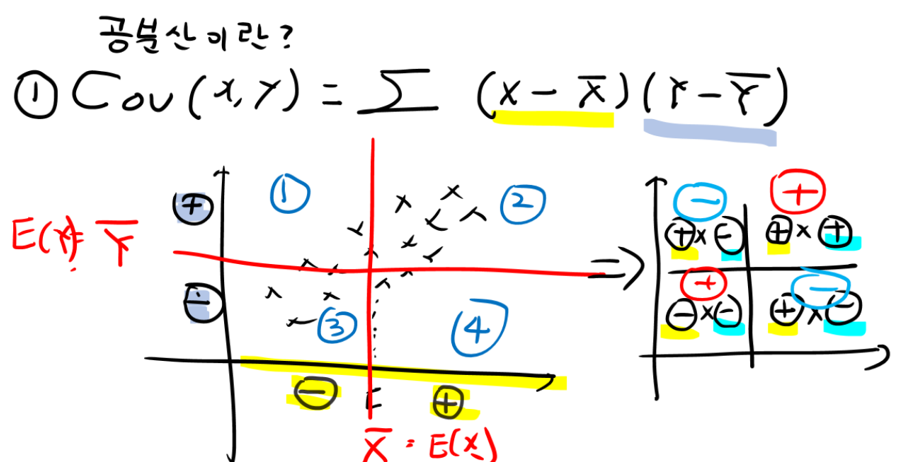
그림과 같이 4가지 영역을 보면 부호를 판정할 수 있습니다.
1번영역 : Y증가(+), X감소(-) ☞음수(-)
2번영역 : Y증가(+), X감소(+) ☞양수(+)
3번영역 : Y감소(+), X감소(-) ☞양수(+)
4번영역 : Y감소(-), X감소(+) ☞음수(-)
Step6) 증가 경향, 감소경향에서의 공분산(Covariance)
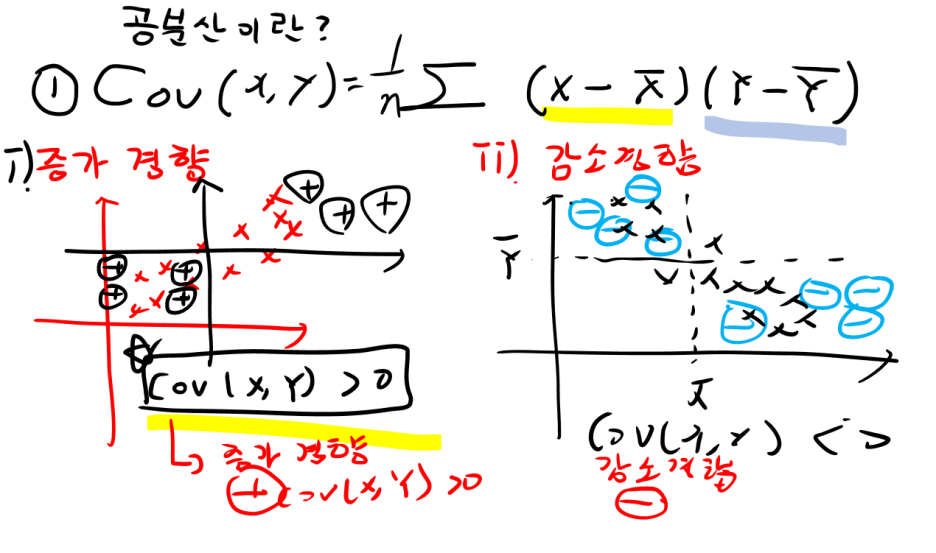
Step5에서 1,2,3,4영역으로 부호를 판정하면 위의 그림으로 이해할 수 있습니다.
분포가 증가 경향 : Cov(X,Y)>0 ☞ (+)
분포가 감소 경향 : Cov(X,Y)<0 ☞ (-)
3. 공분산(Covariance)의 한계
☞ 상관계수(Correlation) 개념
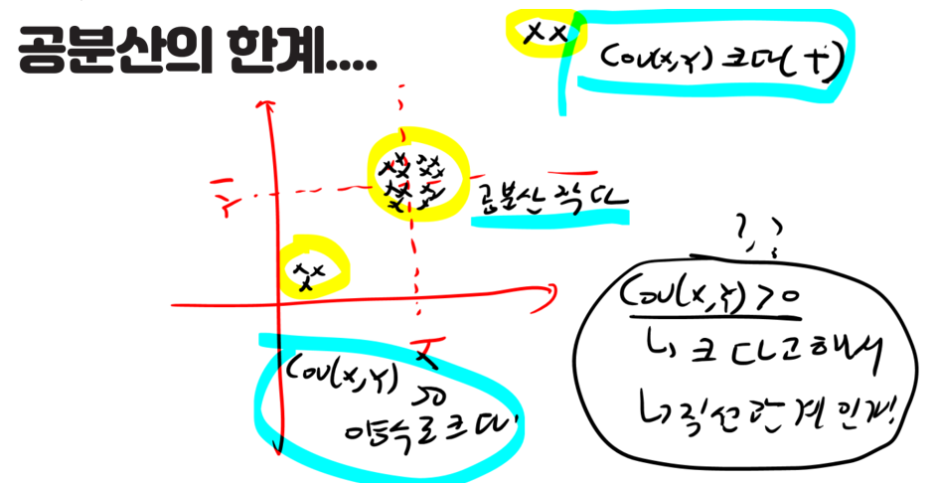
공분산으로 증가, 감소를 이해하면 상관계수라는 개념이 필요없을까요?? 공분산에서는 극단치에 약점? 또는 값이 왜곡되어서 분포모양이 왜곡될 수 있기 떄문에 표준화 된개념이 필요하게 됩니다. 때문에 상관계수의 식을 보면 각각의 표준편차로 표준화하는 과정이 들어가고 이때 상관계수는 -1에서1사이 값을 가지게 됩니다. 다시한번 수식을 보면서 의미를 되새겨 봅니다.
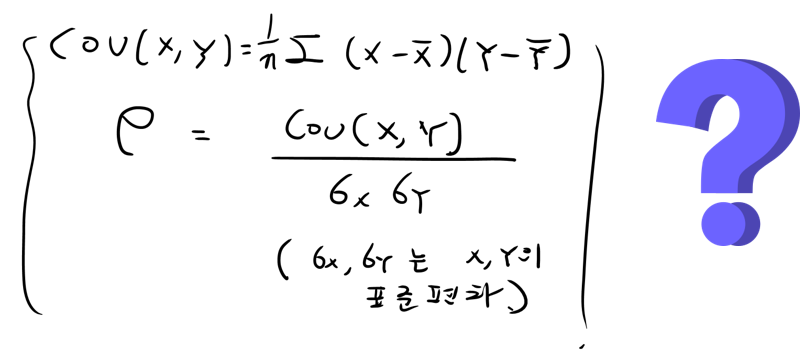
4. 공분산(Covariance) 정리하며....
오늘 포스팅을 준비하면서 상관계수를 넘어가기 전에 공분산의 직관적인 의미를 정리하는데 포커스를 맞추고 준비했습니다. 상관계수는 표준화된 증가, 감소 경향성의 수치라고 이해할 수 있습니다. 다음 포스팅에서는 상관계수의 의미에 대해서 좀더 깊게 정리하고자 합니다.
상관계수에 대해서 다음 포스팅에서는 좀더 자세히 다룹니다.
수학을 전공한 빅데이터를 공부하는 남자 빅공남은 추후 선형대수와 관련해서 쉽게 이해할 수 있는 내용을 정리해보고자 합니다. 오늘 긴 포스팅은 여기서 마치겠습니다.
유튜브 영상으로 공부에
조금이나마 도움이 되는 영상
준비했습니다.
포스팅 맨!! 아래 유트브 링크
첨부합니다.
★구독과 좋아요★
빅공남을 춤추게 합니다 !!
| 선형 회귀분석 기초 쌓기 Linear Regression 이란 무엇인가??? [빅공남! 통계 같이 공부해요] (0) | 2021.12.31 |
|---|---|
| 상관계수 Correlation 이란 무엇인가??? [빅공남! 통계 같이 공부해요] (0) | 2021.12.31 |
| 변수선택(필터/랩퍼/임베디드) [빅공남! 통계 같이 공부해요] (0) | 2021.12.31 |
| 변수 Feature vs Target, Feature Engineering [빅공남! 통계 같이 공부해요] (0) | 2021.12.30 |
| 이상값 이상치 Outlier 탐지 [빅공남! 통계 같이 공부해요] (0) | 2021.12.28 |







댓글