다중공선성 MultiCollinearity 이란 무엇인가??? [빅공남! 통계 같이 공부해요]

다중공선성 Multi-Collinearity란 무엇인가? 다중공선성은 회귀분석 그리고 빅데이터 분석기사 필기 2과목 빅데이터 탐색에서 이해해야하는 중요한 개념 중에 하나입니다. 아래 그림과 같이 분석변수 처리에서 차원축소의 개념이 등장합니다.

특히 선형대수의 차원축소 기법에 대해서 공부하다보면 주성분분석(PCA)라는 기법이 등장하기도 합니다. 대학교 수학인 선형대수학의 행렬과 차원에 대한 이해가 있어야 쉽게 이해할 수 있습니다. 나아가, Eigen Value, Eigen Vector 처럼 고유값, 고유벡터가 무엇인지까지 수학적 개념이 필요합니다. 이에 앞서, 회귀분석에서의 다중공선성의 의미에 대해 이해하면 좋겠다는 생각이 들어서 오늘 포스팅을 준비하게 되었습니다. 유튜브 공부영상 링크는 포스팅 맨 아래 첨부하겠습니다.
1. 회귀분석의 4가지 가정

회귀분석을 적용하려면 4가지 가정이 필요합니다. 바로 위의 그림처럼 정리가 됩니다.
1) 선형성(Linearity)
2) 잔차의 등분산성(Equal Variance)
3) 잔차의 정규성(Normality)
4) 다중공선성 만족하지 않는다(변수의 독립성)
여기서 바로 4번째 가정인 다중공선성을 만족하지 않는다는 것이 어떤 의미인지가 궁금해집니다. 원인 변수가 독립적이어야 한다는 내용인데 오늘 포스팅은 다중공선성에 초점을 맞추고 내용을 전달합니다.
2. Feature vs Target 다중선형회귀???


측 Data Set을 csv 파일로 다운받아서 정리해보았습니다. 데이터 분석에 필요한 Feature는 다음과 같습니다.
[독립변수 : Feature)
1) 임신횟수(Pregnacies)
2) 혈당(Glucose)
3) 혈압(BloodPressure)
4) 삼두근두께(Skin Thckness)
5) 인슐린(Insulin)
6) 체질량지수(BMI)
7) 당뇨병혈통기능(Diabetes PedigreeFunction)
8) 나이(Age)
[결과변수 : Target]
1) 당뇨병 환자 유무 ( False : 0, True 1)
만약 당뇨병 환자 관측이 위의 8가지 요인에 의해서 결정이 된다고 가정을합니다. 당뇨병환자를 유추하는데 만약 8가지 변수로 설명이 된다면 차원은 8이라고 말할 수 있습니다. 그런데... 변수간에 서로 영향을 주는지 안주는지에 따라서 변수가 줄어들 수 도 있지 않을까? 하는 생각을 가질 수 있습니다. 또한 변수간에 선형관계가 있다면 다중선형회귀분석으로 분석을 할 수 있지 않을까? 생각을 할 수 있습니다.
3. 다중공선성(Multi-Collinearity)?
위키피디아에서 다중공선성이 무엇인지에 대해서 찾아보면 다음과 같습니다.
다중공선성(多重共線性)문제(Multicollinearity)는 통계학의 회귀분석에서 독립변수들 간에 강한 상관관계가 나타나는 문제이다. 독립변수들간에 정확한 선형관계가 존재하는 완전공선성의 경우와 독립변수들간에 높은 선형관계가 존재하는 다중공선성으로 구분하기도 한다. 이는 회귀분석의 전제 가정을 위배하는 것이므로 적절한 회귀분석을 위해 해결해야 하는 문제가 된다.
[출처 : 위키피디아]
위키피디아에서 개념을 찾아보면 독립변수들간에 강한 상관관계가 나타나는 문제라고 정의하고 있습니다. 사실 문구로만 봐서는 확실이 개념이 와닿지는 않습니다. 아래 그림을 보면 좀더 감이 올 수 있습니다.

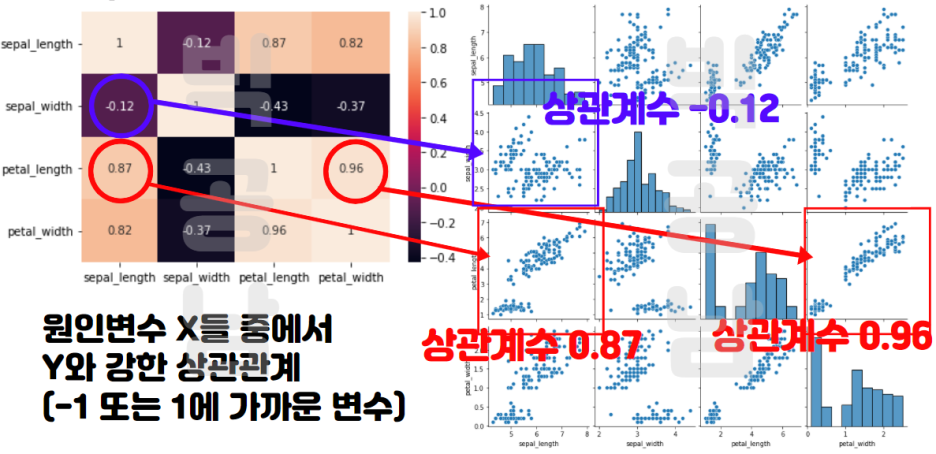
원인변수에 해당하는 변수가 예를 들어서 혈당과 혈압이 있다고 생각을 합니다. 그런데 만약 혈당과 혈압의 상관계수가 높다(상관계수가 1 또는 -1에 가까움)면 두 변수는 거의 같은 변수처럼 움직입니다. 즉, 혈당과 혈압의 직선관계를 안다면, 하나만 측정해서 유추할 수 있습니다. 다중공선성이란 독립변수(Feature)간에 높은 상관관계(상관계수 -1,1)를 가지는 경우를 의미합니다.
4. 다중공선성(Multi-Collinearity) 시각화
다중 공선성의 개념을 좀더 시각화 해서 이해하려면 다음 그림과 같이 이해하면 도움이 됩니다.
1) 다중공선성 NO!!
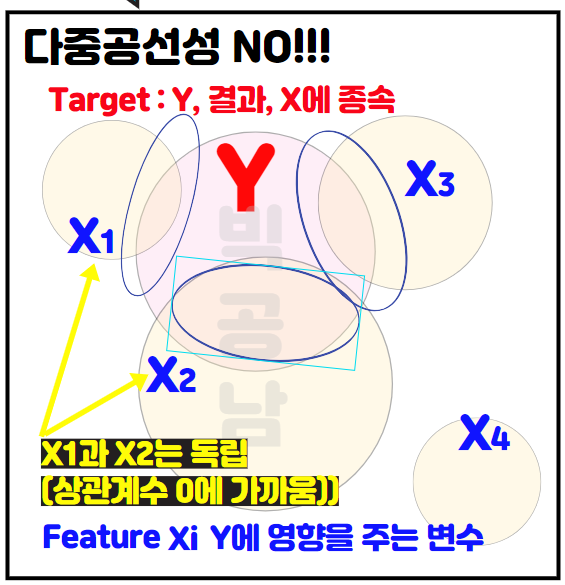
그림과 같이 결과 Y가 X1,X2,X3,X4에 의해서 영향을 받는다고 가정을합니다. 그런데 X4는 Y와 상관계수가 0에 가까워서 Y와의 상관성을 찾을 수 없습니다. X1,X2,X3가 그림에서 Y와 강한 상관관계가 있다고 생각을 합니다. 즉, X1,X2,X3가 각각 상관계수가 1 또는 -1에 가까워서 비례관계의 분포를 가지고 있는 상태입니다. 그런데 X1,X2,X3는 전혀 교집합이 없습니다. 즉, 상관계수(Correlation)이 0에 가까운 것을 의미합니다.
2) 다중공선성 YES !!
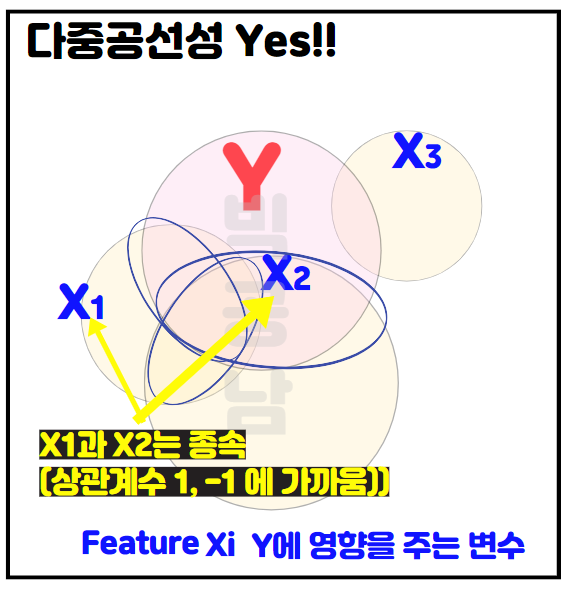
다음 그림과 같이 X1,X2가 Y에 영향을 미치지만 Feature 원인 변수 X1과 X2이 강한 상관관계를 가지는 경우를 나타냅니다. 이 경우에 X1과 X2가 직선관계를 가지기 때문에 한 변수로 설명을 하거나 파생변수를 만들어서 하나의 변수로 만들어 갈 수 있습니다. 위의 그림처럼 Feature간에 상관계수가 높은 경우에는 Target인 Y를 예측하는데 중복된 요인으로 설명하기 때문에 예측하는 설명력?이 낮아질 수 있습니다. 포스팅 서두에 정리한 회귀분석의 가정은 Feature가 다중공선성을 만족하면 안된다는 의미는 결국 변수간 상관관계가 낮아야 한다는 것을 의미합니다.
간단한 방법으로 상관계수를 보려면 상관계수의 히트맵을 보면 됩니다. 히트맵 예시 그림은 다음과 같습니다.
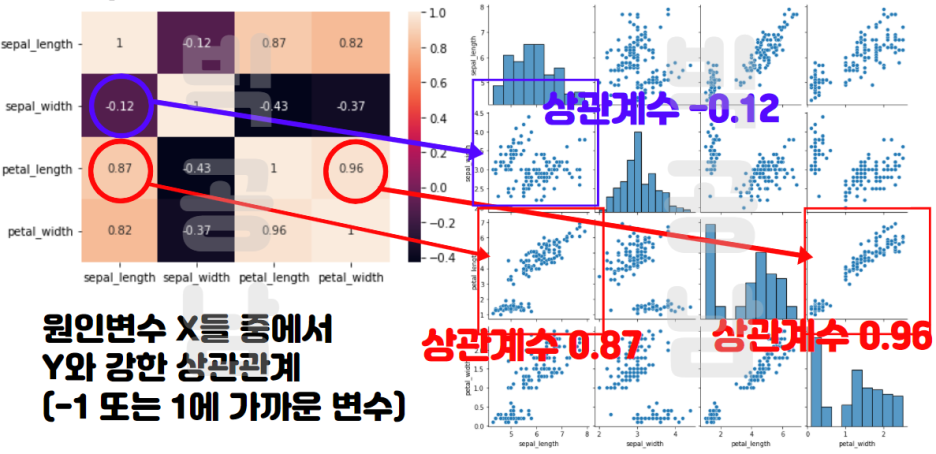
참고로 파이썬으로 상관계수 히트맵을 살펴볼 수 있는 코딩은 아래 포스팅에서 정리를 했습니다. 링크 첨부합니다.

다중 공선성을 만족한다는 것은 결국에 결과(Target)에 영향을 주는 변수인 Feature 간에 상관성이 높은 변수가 있다는 것을 의미합니다.

이는 모형에서 같은 요인을 중복되어 설명할 수 있다는 것을 의미하고 계산량 증가와 예측력(설명력)을 떨어트릴 수 있다는 것을 의미합니다.

즉 차원축소!!!의 필요성이 생길 수 있다는 것을 의미합니다. 그래서 다음 포스팅에서는 변수의 독립과 종속에 대해서 다시 한번 짚고 넘어가고 차원축소에 대해서 설명을 해보고자 합니다.
[빅공남 유트브 채널 바로가기]
[빅공남! 통계 같이해요 바로가기]
[빅공남! 문과생을 위한 고등수학 13강]
| Data = Vector 데이터는 벡터로 표현? [빅공남 통계 같이 공부해요] (1) | 2022.01.08 |
|---|---|
| Vector Dimension 벡터와 차원 [빅공남 통계 같이 공부해요] (0) | 2022.01.06 |
| 다중 선형 회귀분석 Multiple Linear Regression 이란 무엇인가??? [빅공남! 통계 같이 공부해요] (0) | 2021.12.31 |
| 선형 회귀분석 기초 쌓기 Linear Regression 이란 무엇인가??? [빅공남! 통계 같이 공부해요] (0) | 2021.12.31 |
| 상관계수 Correlation 이란 무엇인가??? [빅공남! 통계 같이 공부해요] (0) | 2021.12.31 |







댓글