linear Independent dependent 선형대수 독립 종속 [빅공남! 통계 같이 공부해요]

Vector Linear dependent independent 벡터의 독립과 종속 개념은 차원을 이해하기 위한 중요한 개념중에 하나입니다. 선형대수(Linear Algebra)에 등장하는 독립(Independent)와 종속(dependent)개념을 잘 정리하면 차원과 좌표에 대한 시야를 넓혀갈 수 있습니다. 그래서 데이터 분석에서 차원 축소개념인 PCA 기법 등을 이해하기 앞서 오늘 포스팅과 맨 아래 링크에 있는 유튜브 영상을 보면서 공부를 하면 도움이 될 수 있습니다.
지난 포스팅에서 정리했던 선형결합(Linear Combination 내용을 먼저 공부하고 오늘 포스팅을 이해하는데 도움이 됩니다. 먼저 지난 포스팅 링크부터 첨부하겠습니다.
Vector Linear Combination 선형대수 선형결합 일차결합 [빅공남! 통계 같이 공부해요]
Vector Linear Combination 선형결합 일차결합 개념은 차원을 이해하기 위한 중요한 개념중에 하나입니다. 선형대수(Linear Algebra)에 등장하는 Linear Combination 개념을 오늘 포스팅 주제로 선정했습니다. 데
seeyapangpang.tistory.com
지난 포스팅에서 정리했듯이 벡터의 선형결합으로 2차원 공간을 만들어가는 것을 배웠습니다. 벡터의 덧셈과 스칼라곱의 연산으로 늘리고 줄여서 합성을 하면 새로운 벡터를 만들 수 있었습니다. 오늘 내용의 내용을 요약하면 아래 gif 이미지와 같습니다. 그럼 본격적으로 시작하도록 하겠습니다.

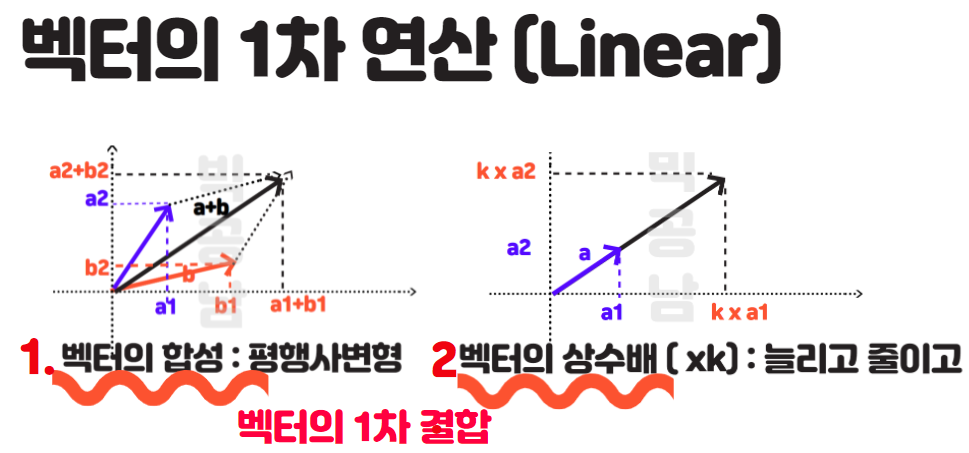
1. 벡터의 1차결합(Linear Combination)
벡터의 1차 결합이란 두벡터의 연산을 덧셈과 스칼라곱으로 만들어 내는 것을 의미합니다. 아래 그림과 같이 2차원 공간에서 좌표로 표현된 위치벡터를 보겠습니다. 아래 그림을 보면 벡터의 두 연산이 이해가 가실 것입니다.
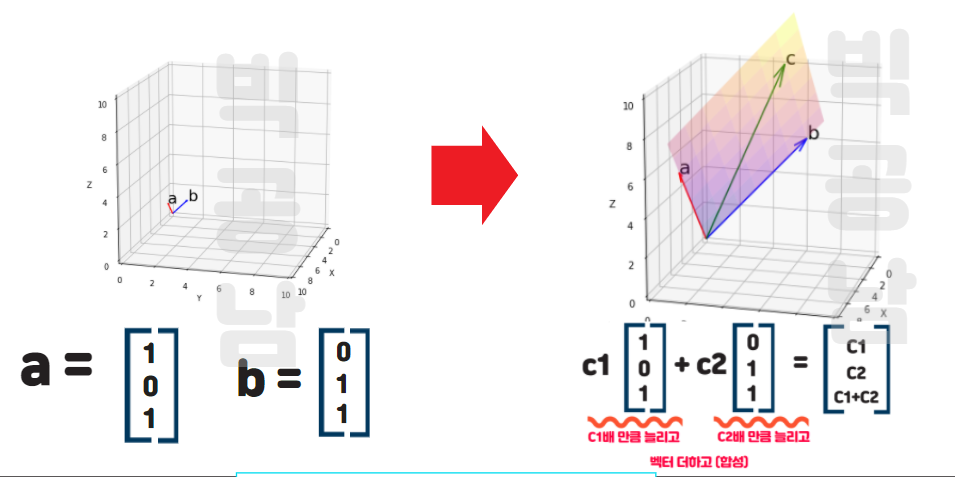
3차원 공간에서 두 벡터의 1차 결합을 하게 된다면 아래와 그림과 같이 평면을 만들어 지는 것을 볼 수 있습니다.
2. 두개의 벡터의 독립과 종속의 개념 이해하기
두 벡터이 독립(Independent)과 종속(dependent)의 개념은 하나의 벡터로 다른 하나의 벡터를 만들 수 있는가? 라는 질문에서 부터 출발할 수 있습니다.

두 벡터를 일차결합으로 다른 벡터를 만들 수 있는지? 에 대한 질문은 결국 두 벡터의 방향이 같은가?에 관한 질문으로 이해할 수 있습니다.

시각적인 이해를 돕고자 아래 2차원 공간에서 2가지 경우의 두 벡터 상황을 그려보았습니다. 아래 왼쪽 그림의 경우 두벡터가 서로 평행한 경우입니다. 서로 평행하다는 것은 상수배만큼 늘리면 다른 하나의 벡터가 될 수 있음을 의미합니다. 그런데 아래 오른쪽 그림을 보면 아무리 하나의 벡터를 늘리고 줄여도 다른 벡터와 같아질 수 없습니다. 평행하지 않기 때문이죠?
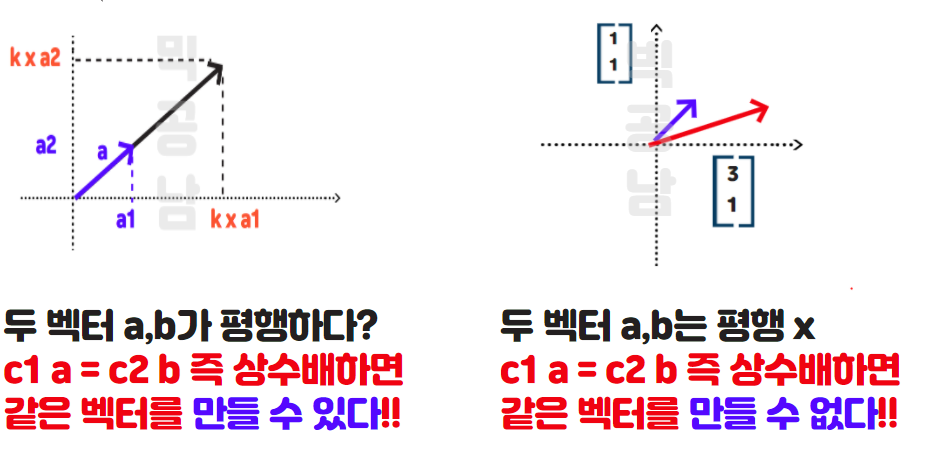
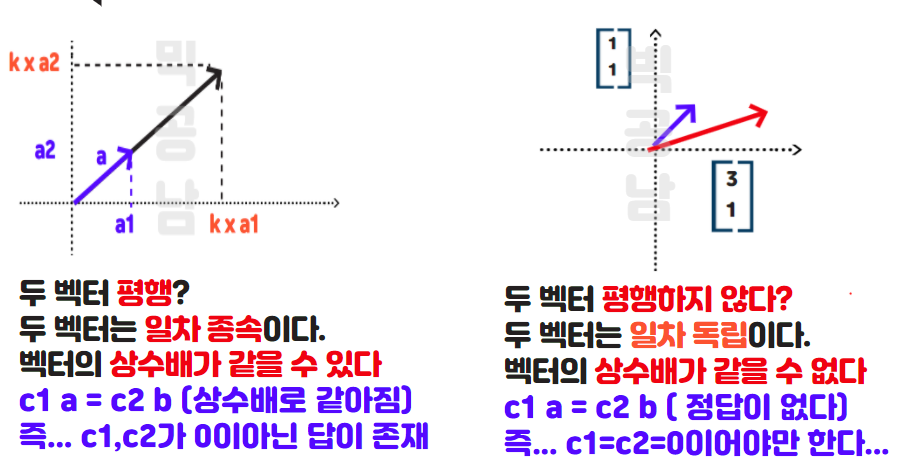
위의 그림처럼 왼쪽은 결국 c1 a = c2 b 를 만족하는 벡터를 찾을 수 있습니다. (서로 늘리고 줄여서 같아 질 수 있음을 의미) 그런데 오른쪽 그림은 c1 a = c2 b를 만족하는 c1과 c2값은 없습니다. 그래서 c1 a = c2 b를 만족하는 c1, c2는 c1=c2=0뿐입니다. 오른쪽 그림처럼 늘리고 줄여서 해가 없는 경우 즉, c1 a = c2 b의 해가 c1=c2=0인 경우를 일차 독립(Linear independent)라고 말하고 왼쪽 그림처럼 c1 a = c2b 를 만족하는 c1, c2의 순서쌍이 0이 아닌 해가 있을 경우 일차 종속(LInear dependent)라고 말합니다. c1, c2의 순서쌍이 0이 아닌 해가 있을 경우는 결국 한벡터를 늘리고 줄여서 다른 벡터가 된다는 것을 의미합니다.
3. 세개의 벡터의 독립과 종속의 개념 이해하기
세 벡터의 일차독립(independent)과 종속(dependent)의 개념을 이해하려면 다음과 같은 질문을 던져보아야 합니다. 두 벡터의 일차결합으로 나머지 다른 하나의 벡터를 만들 수 있는가? (Yes/No)

아래 그림과 같이 3차원 공간에서 3개의 벡터를 가지고 독립과 종속의 개념을 같이 이해하고자 합니다. 먼저 아래 왼쪽 그림에서는 a,b,c 3개의 벡터가 보입니다. c벡터는 지난 포스팅에서 설명드렸듯이, a,b벡터는 평행하지 않습니다. 그래서 2번에 의해서 두 벡터는 일차독립(Linear Independent)입니다. 그런데, c벡터는 a,b로 만들어진 평면 위에 존재하는 벡터입니다. 그래서 c벡터는 a와b의 일차결합으로 표현할 수 있는 벡터이고 이때 a,b,c벡터는 종속되어있다고합니다.
아래 오른쪽 그림에서는 d벡터가 등장합니다. d벡터는 a와b로 만들어진 평면 바깥에 존재하는 벡터입니다. 때문에 a와 b의 일차결합으로 c를 만들 수 없게 됩니다. 이 경우에 a,b,d벡터는 독립(independent)이라고 합니다.
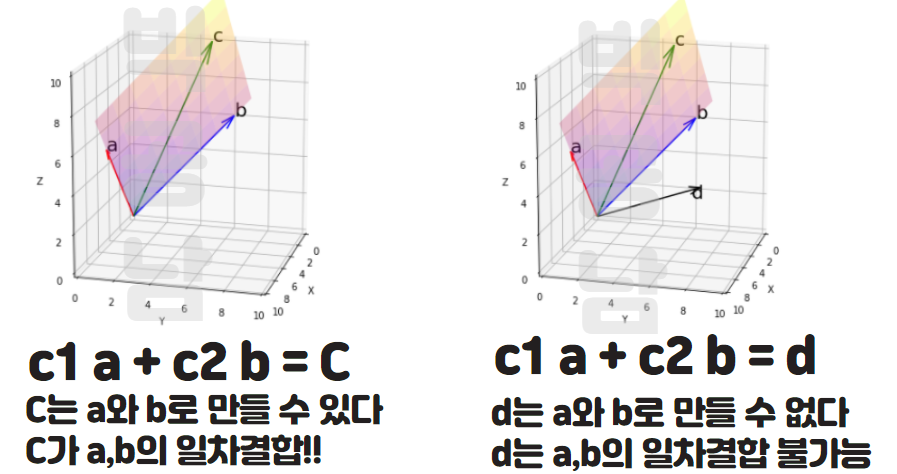
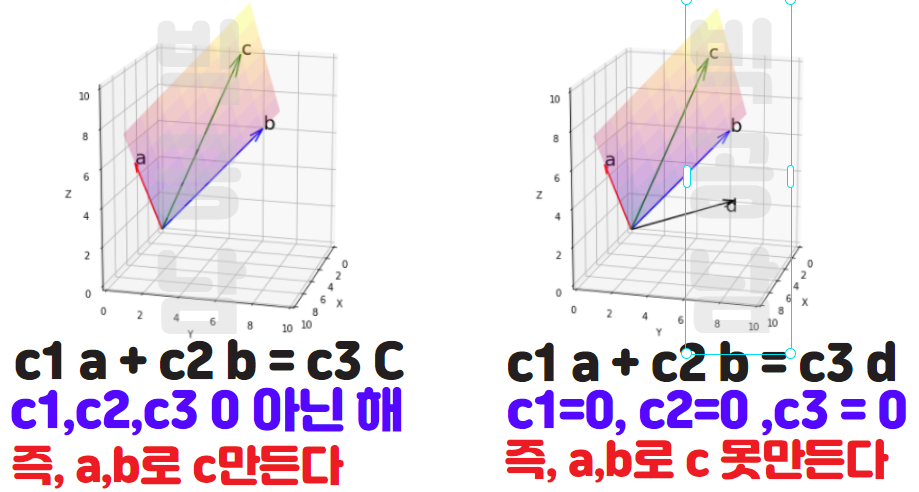
3개 벡터 a,b,c가 일차 종속이라는 것은 c1 a+c2 b = c3 c 를 만족하는 c1,c2,c3가 모두 0은 아닌 해가 존재하는 것으로 이해할 수 있습니다. a,b,d벡터는 일차 독립인데 c1 a+c2 b = c3 d 를 만족하는 c1,c2,c3가 모두 0일 경우만 가능하기 때문입니다.
4. 벡터의 독립과 종속 그리고 데이터분석 차원축소
선형대수에서 벡터의 일차독립과 종속은 중요합니다. 벡터로 만들 수 있는 공간을 몇 차원으로 만들 수 있는가?에 관한 주제입니다. 예를들어 3차원 공간에서 앞어서 다뤘듯이, 3개의 벡터 a,b,c가 있는데 a,b,가 일차 독립이고, 만약 c벡터가 a,b의 일차결합(Linear Combination)으로 만드는 벡터라면 이 공간은 2차원 평면이 됩니다. 즉 a,b가 독립이기 때문에 2차원 공간이 만들어지고 c를 추가하더라도 공간의 차원변화는 없는 것입니다. 이러한 개념을 이용해서 데이터 분석에서 차원축소로 개념을 이어갈 수 있습니다.

'빅데이터 > 통계노트' 카테고리의 다른 글
| Dimension Reduction 차원 축소 이유 Why? [빅공남! 통계 같이해요] (0) | 2022.01.24 |
|---|---|
| 차원축소 변수 독립 종속 dependent independent 선형대수 Linear Algebra [빅공남! 통계 같이해요] (0) | 2022.01.16 |
| Vector Linear Combination 선형대수 선형결합 일차결합 [빅공남! 통계 같이 공부해요] (0) | 2022.01.12 |
| Data = Vector 데이터는 벡터로 표현? [빅공남 통계 같이 공부해요] (1) | 2022.01.08 |
| Vector Dimension 벡터와 차원 [빅공남 통계 같이 공부해요] (0) | 2022.01.06 |




댓글