PCA Principle Component Analysis 주성분분석 [빅공남! 통계 같이해요]

PCA(Principle Component Analysis) 주성분 분석은 차원축소 기법 중 중요한 개념중에 하나입니다. 차원 축소(Dimensional Reduction)는 정사영(Projection)을 통해서 줄일 수 있는데 오늘 포스팅에서는 이 기법의 시각적인 이해화 수식을 100% 정리하지는 않지만 직관적인 의미 정도를 전달하고자 합니다.
먼저 빅공남 통계 23번째 영상에서는 2차원을 1차원으로 축소하는 정사영(Projection)에 대해서 공부했었습니다. 지난 포스팅 링크 먼저 첨부하겠습니다.
정사영 Projection 2d to 1d 2차원 1차원 차원축소 [빅공남! 통계 같이해요]
정사영 Projection 2차원 1차원 차원축소 개념 등에서 중요한 내용 중에 하나입니다. 빅데이터 분석에서 차원을 축소한다는 개념에서 벡터의 정사영 Projection 개념을 이해하면 도움이 됩니다. 2차원
seeyapangpang.tistory.com
2차원을 1차원으로 축소한다는 개념은 데이터의 중심(Center)에서 직선의 방향 즉, 축(Axis)을 잡고 수직인 그림자를 쏘는 것으로 이해할 수 있습니다. 파이썬 코딩을 통해서 직선을 360도 회전을 하면서 1차원 정사영(Projection)이 어떻게 변하는지 그림으로 표현했었습니다.

위의 이미지 처럼 직선에 정사영을 시켜서 1차원 직선으로 데이터의 차원을 축소한 것을 볼 수 있습니다. 이처럼 차원 축소를 하게 되면 원본 데이터의 정보를 잃지만, 간소화 해서 데이터를 볼 수 있는 장점이 생깁니다. 그러면 원본 데이터의 정보의 분산(퍼짐 정도)를 유지하면서 1차원으로 바꾼다는 개념을 어떻게 이해할 수 있는지 보고자 합니다. 이러한 이해는 PCA기법의 가장 중요하고 기본적인 아이디어가 됩니다.

그림에서 축을 45도로 잡을 경우가 대략 분산이 최대로 되면서 데이터의 거리를 보존하는 방향이 되는 것을 알 수 있습니다. 이처럼 PCA 기법은 고차원의 데이터를 저차원으로 바꾸는데 분산이 최대인 축을 잡아 가는 과정에서 출발합니다.
만약 데이터를 2차원으로 축소하려면 데이터의 축이 2개가 필요하게 됩니다.
1. PCA(Principle Component Analysis)란?
PCA(Principle Component Analysis) 기법이란 아래 그림과 같이 고차원의 데이터를 저차원의 데이터로 축(Axis)를 잡고 정사영(Projection)시켜서 데이터의 정보를 바꾸는 것을 의미합니다. 여기서 축은 분산이 최대가 되는 축을 잡고 이 축에 수직이 되는 축을 잡아가는 것을 의미합니다. 그래서 여러 방향중에서 가장 분산이 큰 방향이 PC1이 되고, PC1에 수직이면서 그다음 분산이 큰 방향이 PC2, 그다음 PC3.... 이런식으로 축을 잡아 가게 됩니다. PCA를 2차원으로 한다는 의미는 PC1, PC2 두 축(Axis)가 만드는 공간으로 데이터를 표현하는 것을 의미합니다. 아래 그림과 같이 고차원의 데이터를 2차원으로 축소하게 된 것을 알 수 있습니다. 아래 그림에서 Compoent#1원은 PC1을 의미하고, 가로로 분산이 최대가 되는 방향을 잡아낸 것입니다.

2. PCA 주성분분성과 분산(Variance)
PCA 주성분분석과 분산의 관계를 대략적으로 살펴보는 식을 찾아보았습니다. 중학교때 배웠던 피타고라스 공식을 통해서 1차원 축을 잡는데서 분산을 최대로 한다는 의미를 살펴 볼 수 있습니다. 아래 그림은 특정 사이트에서 찾아 보아서 이해를 돕고자 참고하게 되었습니다.

D3가 원래 데이터까지의 거리를 나타내고 D1은 직선에 정사영 시킨 거리를 나타냅니다. D2는 정사영된 데이터와 원래 데이터 사이의 거리를 의미합니다. 피타고라스 공식에 의해서 다음 식이 성립합니다.
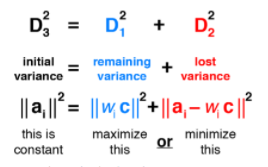
중요한점은 D3^2 = D1^2 + D2^2에서 D3제곱이 더 크다는 것을 알 수 있습니다. 그림에서 보듯이 D1은 원데이터의 직선방향으로 보존된 분산을 가르킵니다. D2는 그러면 원데이터와 정사영데이터의 거리이므로 손실된 분산으로 볼 수 있습니다. 그래서 원래 데이터의 분산은 1차원으로 정사영 시킴으로써 분산을 잃었다고 볼 수 있습니다. 그래서 PCA기법으로 첫번째 축(Axis)를 잡는 다는 것은 보존하는 분산을 최대화(Max), 잃는 분산을 최소화(Min) 방향으로 축을 잡는 것을 의미합니다.
다음 그림처럼 3차원의 공간의 데이터가 있을 때, 2차원 평면으로 정사영 시키면 데이터의 일부 분산을 잃더라도 어느 정도 보존하면서 2차원 평면 데이터로 그려낼 수 있습니다.
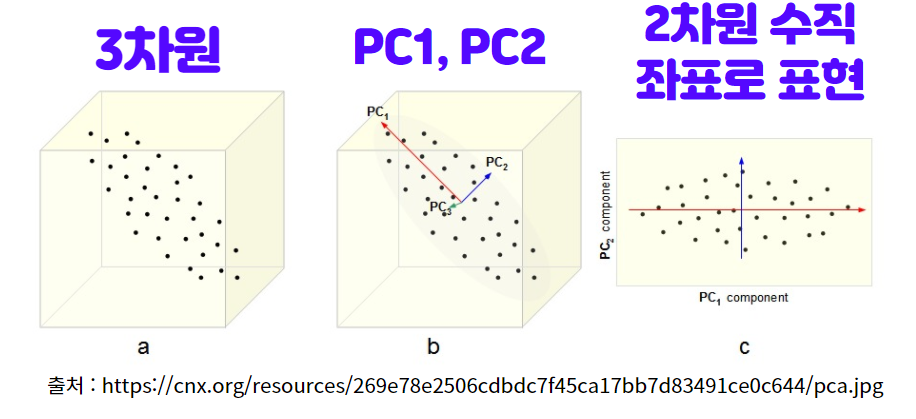
3. PCA 기법 요약
그래서 간단하게 PCA 기법을 위에서 정리한 내용을 바탕으로 아래와 같이 정리해보았습니다.
<Principle Component Analysis>
1) 변동성을 최대한 보존하는 방향으로 주성분 추출(PCA)
2) 직선 방향중 가장 분산이 큰 방향이 PC1
3) PC1에 수직이면서, 그 다음 변동성이 큰 축이 PC2, PC3, PC4...
4) 주성분(저차원)으로 만든 공간으로 사영(Projection)
<PCA 기법을 위한 수학 통계 키워드>
1) 표준화
2) 공분산행렬
3) 고유값(Eigenvector)
4) 고유벡터(Eigenvector)
PCA기법에는 수학/통계 요소가 내재되어 있고, 계산은 파이썬 코딩을 활용해서 살펴볼 수 있습니다.
4. PCA 계산 어떻게 HOW?
PCA기법을 계산하는 방법은 다음과 같습니다.
1) 데이터 표준화 ( x-m/시그마) : z-socre
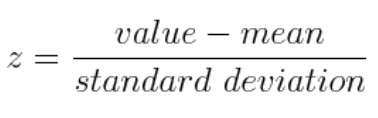
2) 변환된 데이터의 공분산 행렬 계산
3) 행렬의 고유값, 고유벡터 계산
공분산행렬 A에 대하여,
Ax = λx인 λ, x 찾기
4) 고유값이 큰 벡터부터 PC1, PC2, PC3...
5) 원래 Data를 주성분(PC1,PC2...) 좌표로 회전 및 표현
그러면 PCA기법을 대략적으로 이해하는 그림을 찾아보았습니다. 아래 그림을 보면 시각화해서 이해할 수 있습니다.
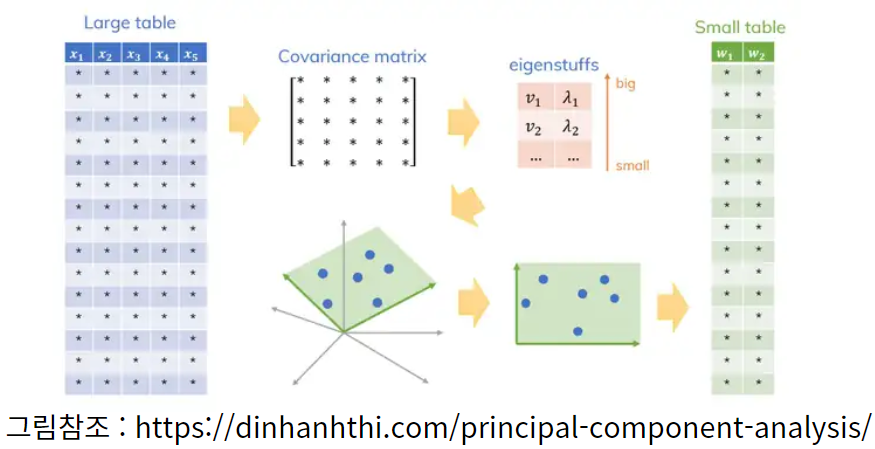
그림에서 보면 데이터는 5차원 데이터를 가지는 상황입니다. 데이터 표본(Sample)은 15개가 존재합니다. 벡터 관점에서 바라본다면 5차원 벡터 15개가 존재하는 상황입니다. 각 데이터를 표준화 변환을 해서 평균을 0으로 맞추고, 공분산 행렬을 계산합니다. 이행렬의 고유값(Eigenvalue)와 고유벡터(Eigenvector)를 계산합니다. 수학적 수식으로 이해하는 내용은 추후 포스팅에서 다루고자합니다. 오늘 포스팅에서는 PCA기법을 하게 되면, 행렬문제를 풀면 된다 정도로 받아드리고자합니다. 공분산행렬의 고유값이 클때의 고유벡터가 PC1이 됩니다. 그 다음 고유값이 큰방향으로 PC2가 되도록 잡아가면 됩니다. 여기서 중요한 부분은 고유값이 큰 방향이 분산이 큰 방향이라는 것입니다.
5. PCA기법과 Explaind Ratio
PCA기법에서 중요한 부분은 Explaind Ratio입니다. 수학적 수식 증명을 통해서 고유값의 비율이 특정 데이터를 나타내는 비율이 됩니다. 이러한 사실을 이용하면 공분산행렬을 통해서 EigenValue를 찾아낼 수 있고 이 값을 통해서 원본데이터의 분산(Variance)를 몇% 보존하는가?를 나타낼 수 있습니다. 그래서 이러한 개념이 Explaind Ratio가 됩니다.

그래서 공분산 행렬의 수학적 계산을 통해서 원본데이터의 분산 설명 비율(%)를 계산해 낸다는 것이 아주 중요한 사실입니다. 이러한 접근 방법은 주성분을 몇개 선택할지?와 연결이 됩니다. 주성분을 많이 사용할 수록 데이터가 복잡해지면서 원본데이터의 분산을 더 많이 설명하게 되는데, 어느 정도까지 선택을 할지와 연관이 됩니다.
6. PCA기법 구글 코랩 파이썬 코딩으로 살펴보기
PCA기법을 파이썬에서 간단하게나마 이해해보고자 코딩을 만들어 보았습니다. 아래와 같이 파이썬에서 데이터를 만들고 공분산 행렬을 만들어 보았습니다. 아래 공분산 행렬을 보면 특정값이 크게 나오는 것을 알 수 있습니다. 공분산행렬을 스케일(Scale)변환 없이 그대로 사용하게 된다면, 절대치에 영향을 받게 되어서 편향(Bias)이 발생할 수 있습니다. 때문에 먼저 데이터의 Scale을 Z-score로 변환부터 합니다.

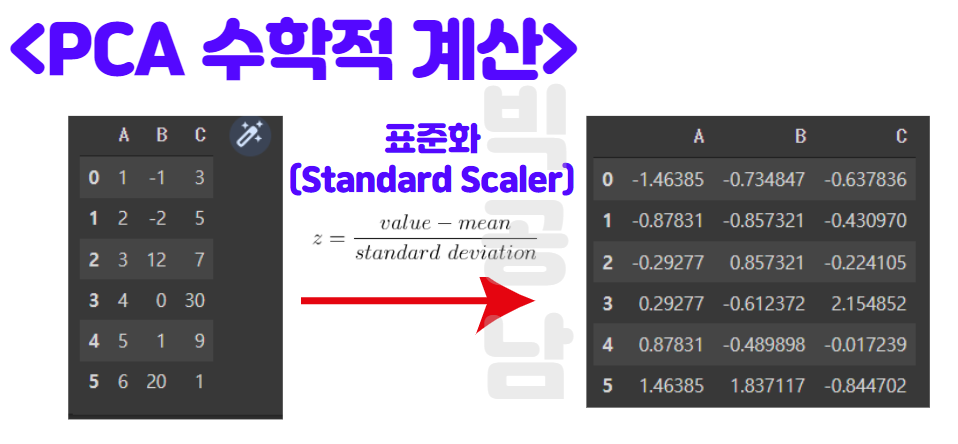
아래 그림과 같이 A,B,C 변수로 이루워진 3차원 데이터를 Standard Scale로 변환을 해서 데이터를 자시 표현하면 오른쪽 그림과 같이 표현할 수 있습니다.
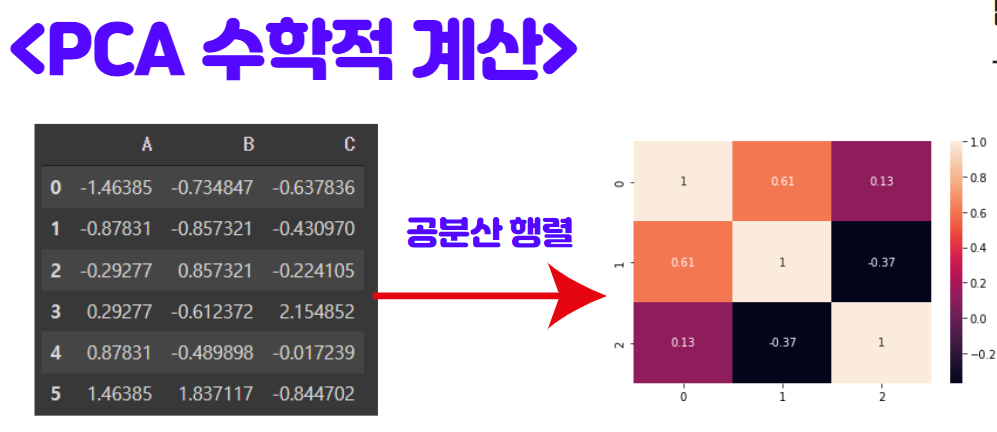
아래 그림과 같이 Standard Scale로 표준화 된 데이터의 공분산 행렬(Covariance Matrix)를 계산하였습니다.
이제 데이터의 고유값, 고유벡터 문제를 풀면, 분산이 최대인 고유벡터와 고유값을 찾아낼 수 있습니다.

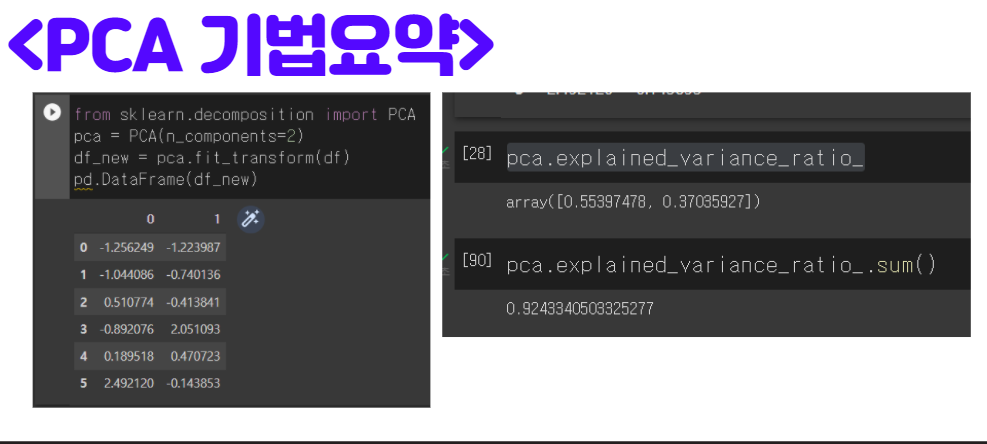
아래 그림과 같이 싸이킷런의 PCA기법 모듈을 불러와서 PCA 계산을 한번에 해낼 수 있습니다. 여기서 중요한 부분은
PCA(n_compoenent=2)라는 명령어는 2차원으로 축소한다는 의미입니다. 만약 3차원으로 축소하려면 PCA(n_compoenent=3)이라고 명령어를 쓰면됩니다.
특히나 아래 그림에서 주의깊게 볼 명령어는 pca.explainex_variance_ratio_입니다. 아래 그림과 같이 명령어로 계싼하면
결과가 [0.55,0.37]이 나옵니다. 중요한 점은 이 숫자가 원본 데이터의 분산을 설명하는 비율을 가르킵니다. 각각 55%, 37%의 숫자를 나타내기 때문에, 합치면 92% 정도의 분산을 설명한다고 볼 수 있습니다. 그래서 2차원 축소를 통해서 8%의 분산 손실이 있었고, 92%의 분산을 보존하는 차원축소가 되는 것입니다.
이번에는 PCA명령어가 아니라 그대로 Eigencvector, Eigenvalue를 구하는 파이썬 명령어를 통해서 살펴볼 수 있습니다. 바로 다음과 같습니다. 다음과 같이 넘파이 명령어로 eigen_value, eigenvector를 계산해 낼 수 있습니다.
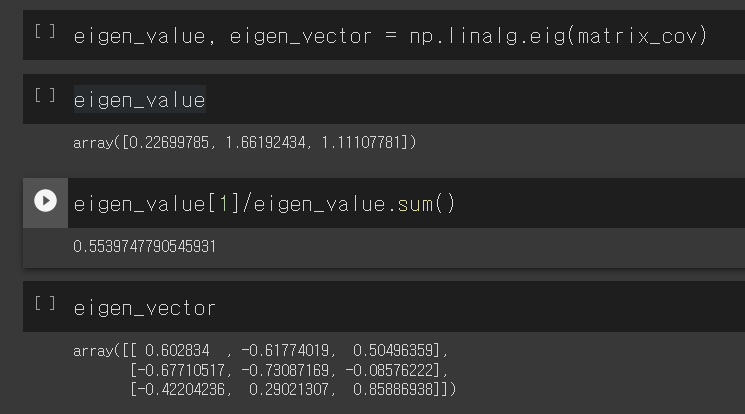
Egien value의 최대값을 eigen vector의 총합으로 나누값이 0.55 즉, 55%가 됨을 알 있습니다. 그런데 이것은 싸이킷런의 PCA모듈을 이용한 값과 일치합니다. 다시 한번 아래 그림을 보겠습니다.

그림처럼 pca.explained_variance_ratio_ 명령어를 통한 55%와 일치하는 것을 확인 할 수 있습니다. 이처럼 PCA기법을 활용하면 원본데이터의 분산을 얼마나 보존하는지 알아낼 수 있습니다.
이처럼 PCA기법은 행렬의 고유값, 고유벡터를 계산해서 주성분(PCA)를 계산하고 분산의 몇%를 보존하고 있는지도 같이 알아낼 수 있는 것입니다.
그래서 다음 포스팅에서는 Explained Ratio를 그래프로 시각화하는 방법에 대해서 알아보고자합니다.
[빅공남 유트브 채널 바로가기]
[빅공남! 통계 같이해요 바로가기]
[빅공남! 문과생을 위한 고등수학 13강]
| LDA Linear Discriminant Analysis [빅공남! 통계 같이해요] (0) | 2022.02.14 |
|---|---|
| Scree Plot PCA Eigenvalue Explained Ratio [빅공남! 통계 같이해요 ] (0) | 2022.02.09 |
| Feature Selection Feature Extraction 차원축소 PCA LDA t-SNE SVD [빅공남! 통계 같이해요] (0) | 2022.01.29 |
| Vector Inner Product Dot Product 벡터 내적 선형대수 [빅공남! 통계 같이해요] (0) | 2022.01.27 |
| 정사영 Projection 2d to 1d 2차원 1차원 차원축소 [빅공남! 통계 같이해요] (0) | 2022.01.25 |







댓글