Scree Plot PCA Eigenvalue Explained Ratio [빅공남! 통계 같이해요 ]

Scree Plot PCA Principle Analysis Explained Ratio Eigenvalue Covariance Marix 차원축소 공부에 도움되는 내용을 다루고 있습니다. 오늘 포스팅에서는 Scree Plot에 대해서 정리를 해보고자합니다. Scree Plot은 PCA 주성분분석에서 고유값의 비율(Explained Ratio)를 차트로 시각화한 것입니다.
먼저 오늘 포스팅을 공부하기 앞서 빅공남 통계 26번째 영상에서 PCA 기법에 관한 내용들을 공부하고 Scree Plot을 보시면 도움이 되실 것입니다. 지난 포스팅 링크 먼저 첨부하도록 하겠습니다.
PCA Principle Component Analysis 주성분분석 [빅공남! 통계 같이해요]
PCA(Principle Component Analysis) 주성분 분석은 차원축소 기법 중 중요한 개념중에 하나입니다. 차원 축소(Dimensional Reduction)는 정사영(Projection)을 통해서 줄일 수 있는데 오늘 포스팅에서는 이 기법..
seeyapangpang.tistory.com
PCA기법은 분산이 최대가 되는 축(Axis)를 잡고 수직인 방향의 축을 잡아가는 과정을 의미합니다. 분산의 크기로 순서대로 PC1,PC2,PC3, ... 이렇게 잡아가게 됩니다. 이러한 주성분(PC1,PC2,...)을 찾기 위해서 공분산행렬을 계산하고 공분산행렬의 고유값 계산을 하게 됩니다. 오늘은 파이썬 코딩실습으로 얻어낸 데이터와 차트로 그림을 보면서 이해하고자 합니다.

1. PCA 공분산행렬 고유값(Eigenvalue)
PCA 주성분분석에서 차원을 축소하기 위해서 공분산행렬을 계산하게 됩니다. 공분산행렬의 고유값(Eigenvalue)를 계산하게 되고 이때 고유값이 의미하는 것은 분산이 최대가 되는 방향의 분산 설명 비율 (Explained Ratio)가 됩니다. 이 비율은 n번째 고유값을 전체 고유값의 합으로 나눈 값을 계산하면 알아낼 수 있습니다.
아래와 같이 데이터를 가지고 공분산행렬을 만들어 보았습니다.

데이터를 표준화하고나서 공분산행렬을 만든다면 다음과 같이 코딩으로 결과를 만들 수 있습니다.

데이터를 표준화하고나서 공분산행렬을 만든다면 다음과 같이 코딩으로 결과를 만들 수 있습니다.

다음 싸이킷런 라이브러리의 PCA를 가지고와서 PCA를 해보면 고유값의 비율을 계산해낼 수 있고, 이 값들이 Explained Ratio가 됩니다.
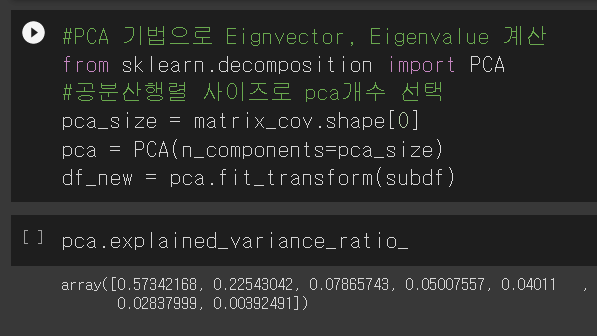
2. Scree Plot ( PCA Eigenvalue로 % Variance 시각화)
Scree Plot 은 각 주성분(PCA)에 해당하는 고유값의 % 비율을 차트로 그려낸 것을 의미합니다. PCA 순서대로 y좌표를 막대그래프로 그려봅니다. 아래와 같이 코딩을 작성해보면 그림을 그려볼 수 있습니다.

다음과 같이 스크리 Plot을 그려냅니다. 첫번째 고유값부터 차원축소를 하면서 각 축으로 사영(Projection)시킬 때 분산의 설명 비율 (Explained Ratio)를 시각화해서 눈으로 빠르게 확인할 수 있습니다.
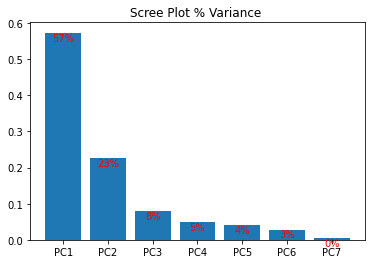
위 그래프 예제에서 살펴보면, PC1에서는 분산을 57% 보존한다는 것을 알 수 있습니다. PC2는 23% 보존하는 것을 알 수 있습니다. 그러면 만약 PC1과 PC2로 데이터를 사영(Projection)시켜서 차원축소를 한다면, 80% 데이터를 보존하면서 축소 할 수 있다는 것을 알 수 있습니다. 이처럼 Scree Plot을 그리게 되면 PCA 주성분분석에서 차원을 얼마나 축소해야하는지 시각화해서 빠르게 이해할 수 있습니다.
3. Accumulated Scree Plot ( PCA Eigenvalue로 % Total Variance 시각화)
이번에는 좀더 나아가서 혼합차트를 그리고자합니다. 꺾은선 그래프로 % Variance를 누적해서 합산한 그래프를 같이 그려넣습니다. 코딩을 해서 그림을 그려보면 아래와 같은 그래프를 얻어 낼 수 있습니다.
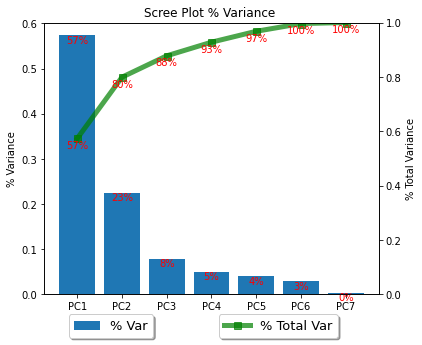
위의 그래프에서 꺾은선그래프를 살펴보겠습니다. PC1, PC2 순으로 축을 잡아가면 갈수록 누적 % Variance가 증가하는 그래프를 볼 수 있습니다. PC3까지의 Explained Ratio를 살펴보면 93%가 됨을 알 수 있습니다. Accumlated Scree Plot을 그리게 되면 축(Axis)을 늘려가면서 몇%까지 설명하는지 쉽게 볼 수 있습니다. 위의 그래프를 보면, 일정 수준이 넘어가면 Variance이 누적 꺾은선 그래프의 기울기가 급격히 줄어드는 것을 알 수 있습니다. PC4부터는 차원을 늘리더라도 % Variance가 크게 변하지 않는 것을 알 수 있습니다. 그래서 차원을 늘리기보다 적당한 수준에서 차원축소를 하면 된다는 것을 쉽게 시각화해서 볼 수 있습니다.
4. Scree Plot과 PCA 차원축소(몇차원까지?)
PCA 기법은 결국 공분산행렬의 고유값의 비율(%)을 계산해서 분산의 Expained Ratio를 계산해내야 하는 것입니다. Scree Plot을 활용해서 2가지 관점에서 몇차원까지 축소를 해야하는 지표로 쓸지 생각해볼 수 있습니다.
1) 누적 비율(%)가 70~90%정도 될때 까지
2) 차원 축소의 기울기가 급격히 완만해 질때 까지
위의 2가지는 꺾은선 그래프를 보면서 쉽게 이해할 수 있습니다.
오늘 포스팅을 위해 파이썬 코딩을 통해서 Scree Plot을 작성해보고 Explained Ratio 개념과 차원을 몇차원까지 축소할 것인가?에 대해서 공부해보았습니다. 다음 포스팅에서는 차원 축소 기법중에 하나인 LDA에 대해서 다루고자 합니다.
| SVD Singular Value Decomposition 특이값분해 [빅공남! 통계 같이해요] (1) | 2022.02.24 |
|---|---|
| LDA Linear Discriminant Analysis [빅공남! 통계 같이해요] (0) | 2022.02.14 |
| PCA Principle Component Analysis 주성분분석 [빅공남! 통계 같이해요] (0) | 2022.02.05 |
| Feature Selection Feature Extraction 차원축소 PCA LDA t-SNE SVD [빅공남! 통계 같이해요] (0) | 2022.01.29 |
| Vector Inner Product Dot Product 벡터 내적 선형대수 [빅공남! 통계 같이해요] (0) | 2022.01.27 |




댓글