Box Cox Transformation 파이썬 박스 콕스 변환 Skew 조절 [빅공남! 통계 같이해요]

Box Cox Transformation 파이썬 박스 콕스 Skew 조절 함수 변환에 대해서 공부하는 포스팅과 유튜브 영상을 준비했습니다. Box Cox 변환은 특히 지난 시간에 공부했던 지수,로그,루트,역수 변환 등 데이터의 함수변환을 포괄하는 개념으로 적절한 변환으로 정규분포에 가깝도록 만드는 분포입니다. 먼저 오늘 Box Cox Transformation을 공부하기 앞서, 지난 포스팅의 함수변환에 관한 내용을 공부하고 오늘 포스팅과 유튜브 영상을 보시면 도움이 되실 것입니다.
지난 포스팅 링크는 아래와 같습니다.
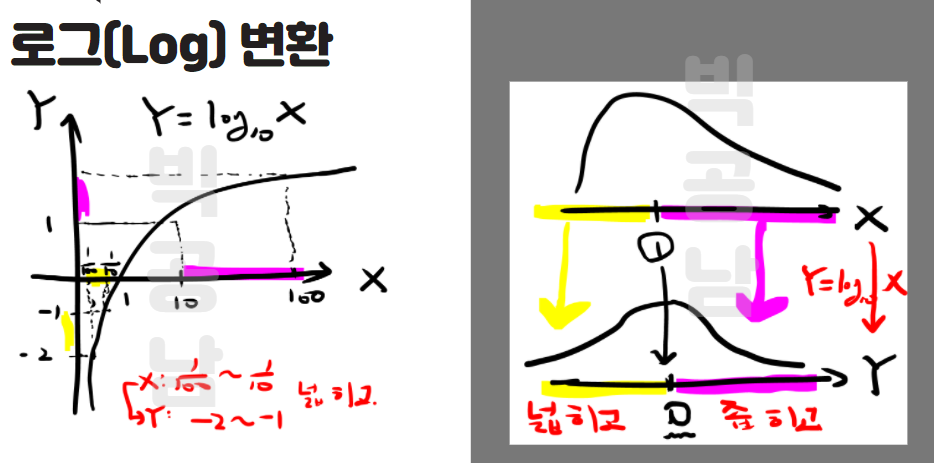
Log Transformation 로그/지수/제곱/루트/역수 함수변환 [빅공남! 통계 같이해요]
Log Transformation 로그 지수 루트 역수 제곱 변환 등 데이터의 변수 변환 기법 중에 하나인 함수 변환에 대해서 같이 공부하는 포스팅과 유튜브 영상을 준비했습니다. 특히, 로그 변환은 Data의 Skew를
seeyapangpang.tistory.com
오늘 Box Cox Transformation에 관한 공부는 이론적인 공부와 파이썬 코딩을 같이 실습해볼 수 있도록 영상을 준비했습니다. 본격적으로 하나씩 차근차근 정리해보고자 합니다.
1. Box-Cox 변환이란?
Box-Cox 변환은 분포의 Skew를 조절하기 위한 변환 중에 하나입니다. 지난 포스팅에서 공부했던 로그, 지수, 역수, 루트 변환과 관련이 있습니다. 지난 시간의 주제는 각 함수변환에 의한 Skew 변환 방향에 대해서 정리를 했었고, Box-Cox 변환의 주된 주제는 임의의 분포를 어떻게 정규분포에 가깝게 변환할 수 있을 것인가? 에 관한 주제입니다. 박스 콕스 변환과 관련된 식은 아래와 같습니다.
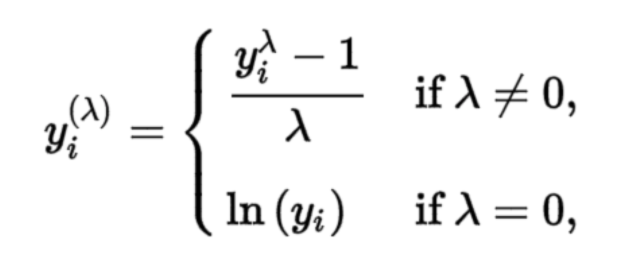
그림을 보면 먼저 람다가 0일때와 람다가 0이아닐때로 구분 되어 있는 것을 알 수 있습니다. 데이터 y에 대해서 람다가 하나 주어지면 하나의 함수변환이 되는 것입니다.
2. Box-Cox 변환, 람다(λ) 파라메터(Parameter)
박스 콕스 변환에서 람다가 하나 결정이 되면, 변수 변환이 결정 되는 것입니다. 즉, 람다는 파라메터(Parameter)로 볼 수 있습니다. 어떤 람다를 쓰느냐에 따라서 다른 변환이 될 수 있는 것입니다. 대략적으로 이해를 돕고자 람다에 간단한 숫자를 넣으면서 어떤 함수변환이 되는지 정리해보았습니다.

예를들어, 다음과 같이 람다를 변환하면,
람다(λ) = +2 : 이차함수
람다(λ) = +0.5 : 루트 변환
람다(λ) = +0 : 로그 변환
람다(λ) = -1 : 역수 변환
함수가 됩니다.
아래 사이트에서 람다에 따른 함수변환이 잘 정리가 되어있어서 첨부하도록 하겠습니다.
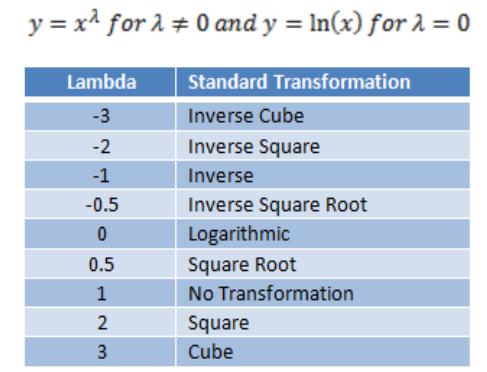
3. Box-Cox 변환, Skew, Optimal Lambda
위에서 설명 드렸듯이, 어떤 람다를 사용하느냐에 따라서 Skew가 바뀌는 정도가 달라지게 됩니다. 그러면 자연스럽게 어떤 람다를 선택해야만 정규분포에 가까운 모양의 분포가 될 수 있을까? 라는 질문이 떠오를 수 있습니다.
그래서 Box-Cox와 관련된 이슈는 정규분포에 관련한 Optimal Lambda를 어떻게 찾을 것인가?에 관한 주제가 될 수 있습니다. 오늘 포스팅에서는 Optimal Lambda를 찾는 방법에 대한 내용보다 파이썬 코딩 결과로 Optimal Lambda의 결과가 어떻게 될지에 대해서 포커스를 맞추고 정리를 해보고자 합니다.

4. Box-Cox 변환과 결과해석
파이썬으로 Box Cox 변환을 하면서 아래와 같은 결과를 얻어냈습니다. 지수분포(Exponential)로 데이터 샘플을 만든 후, Box Cox 변환을 통해서 아래와 같은 결과를 얻고 차트를 그려보았습니다.
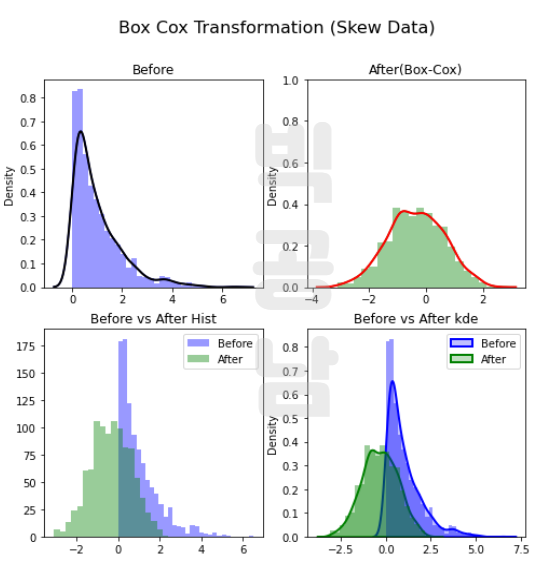
Before에는 오른쪽으로 꼬리가 긴 Positive Skew를 가지는 분포였습니다. 그런데 Box-Cox 변환을 적용한 후 좌우대칭인 정규분포에 가까운 모양이 되었습니다. 파이썬 코딩을 통해서 Skew가 0에 가까운 Optimal Lambda를 찾았고, 이떄 차트를 그려보면 정규분포에 가까운 모양이 되는 것을 확인할 수 있습니다. Before와 After그래프를 보시면 높이는 낮아지면서 좌우 대칭인 분포로 모양이 변하는 것을 확인할 수 있습니다.
이번에는 람다를 바꿔가면서 분포가 어떻게 Skew가 바뀌는지 테스트 해보았습니다.
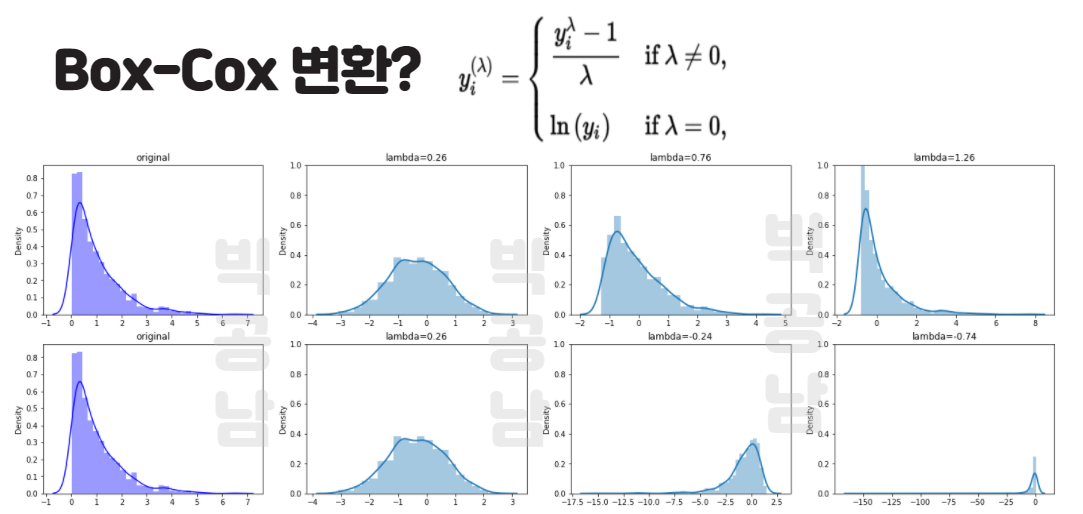
위의 그림처럼 람다가 Opitmal Lambda는 0.26이 되고 좌우 대칭이 됩니다.
Lambda를 0.26 ☞ 0.76 ☞ 1.26 으로 숫자가 커지면,
점점더 오른쪽 꼬리가 긴 Positive Skew그래프가 됩니다.
Lambda를 0.26 ☞ -0.24 ☞ -0.74 으로 숫자가 커지면,
점점더 오른쪽 꼬리가 긴 Negative Skew그래프가 됩니다.
이처럼, Box Cox 변환에서 람다를 변환시킨다는 것은 분포의 Skew를 조절하겠다는 의미가 되고, Optimal Lambda는 가장 정규분포에 가까운 분포를 의미합니다.
6. 파이썬 Scipy boxcox vs boxcox1p
Scipy에서 boxcox관련 명령어는 2가지로 살펴볼 수 있습니다.
[sciypy.stats.boxcox]
scipy.stats.boxcox — SciPy v1.8.0 Manual
docs.scipy.org
위의 사이트에 가서 box-cox 명령어에 대해서 살펴보면, 아래와 같이 변환을 한다고 합니다. Box Cox 명령어는 변환을 통해 변환된 분포와 그떄의 Optimal 람다를 찾아내는 명령어입니다.
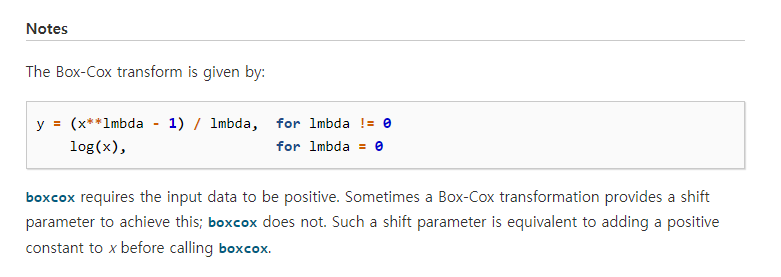
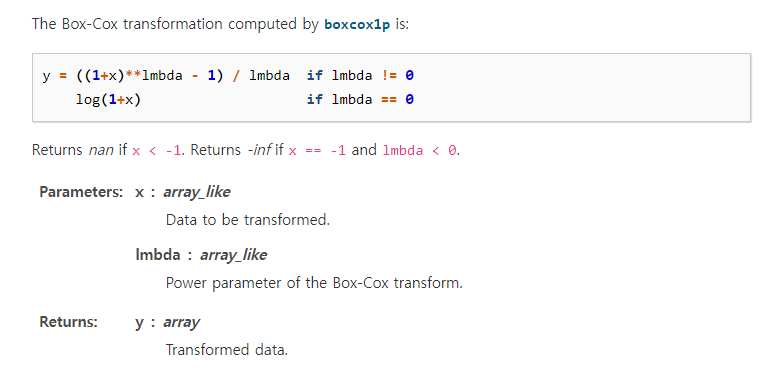
이번에는 Box Cox 1p 명령어를 사려보겠습니다. Box Cox 1p는 원포인트 박스콕스라고 생각하시면 됩니다. 그래서 하나의 람다를 주면 거기에 대한 변환을 해주는 명령어입니다.
scipy.special.boxcox1p — SciPy v1.8.0 Manual
docs.scipy.org
특히나 아래 함수에서 (1+x)**lmbda-1 이부분을 주의깊게 보셔야합니다. 1p boxcox 명령어는 boxcox 명령어와 다르게 x+1이 들어가기 때문에 boxcox 명령어와 같은 조건에서 비교를 해보시려면 변수에 x-1을 넣어야만 같은 결과를 얻을 수 있습니다.
7. 파이썬 Scipy Box Cox 간단한 파이썬 코딩 실습
박스 콕스 명령어로 데이터 변환을 간단히 해보도록 하겠습니다. 먼저 데이터 샘플을 다음과 같이 만들도록합니다. 넘파이의 np.random 함수에서 지수분포로 exponential을 붙여서 데이터 샘플을 만들어 보았습니다.
import numpy as np
from scipy import stats
import seaborn as sns
import matplotlib.pyplot as plt
# create some random data
x = np.random.exponential(size=1000)
# y optimal box cox transform
# optimal lambda (similar zero)
y, lambda_optimal = stats.boxcox(x)
print(lambda_optimal)위의 명령어에서 주의깊게 볼 부분은 바로 박스콕스의 결과를 변환된 y와 optimal lambda를 동시에 얻는 다는 것입니다. 아래 그림과 같이 코딩 실행을 하면 lambda를 확인해 보실 수 있습니다.
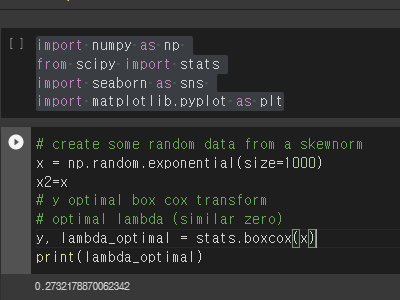
변수 y에는 박스콕스로 변환된 데이터가 저장이 됩니다. 이번에는 boxcox1p코딩을 간단하게 실습해보고자 합니다. 이번에는 다음과 같이 코딩을 입력해봅니다.
from scipy.special import boxcox1p
lambda_select = 0.7
y = boxcox1p(x-1,lambda_select)
print(lambda_select)lambda_select는 사용자가 임의로 값을 넣으면 됩니다. 다시 한번 설명드리지만, boxcox1p에서는 x가 아닌 x-1을 넣어야만 같은 조건의 x에 대해서 비교를 해볼 수 있습니다. 그래서 아래와 같이 람다는 당연히 0.7이 나올 것입니다.
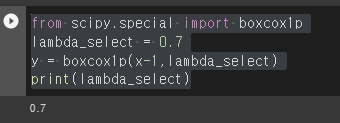
하지만 두 함수의 변환된 y는 람다가 다르기 때문에 그래프는 다르게 나올 것입니다.
차트를 실습해보기 위해서 다음과 같이 실습해보겠습니다. 먼저 원본데이터의 히스토그램을 아래와 같이 그려봅니다.
sns.distplot(x,hist=True, kde=True,color ="blue")
이번에는 박스콕스 변환 이후 그림을 그려보겠습니다.
# create some random data from a skewnorm
x = np.random.exponential(size=1000)
x2=x
# y optimal box cox transform
# optimal lambda (similar zero)
y, lambda_optimal = stats.boxcox(x)
sns.distplot(y,hist=True, kde=True,color ="green")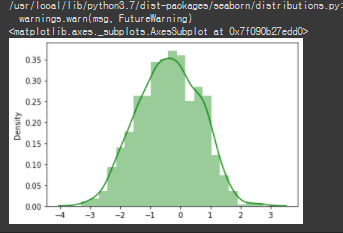
boxcox 1p 명령어로 람다가 0.7일 경우 박스콕스 변환된 그래프는 다음과 같이 실습해봅니다.
from scipy.special import boxcox1p
lambda_select = 0.7
y = boxcox1p(x-1,lambda_select)
sns.distplot(y,hist=True, kde=True,color ="red")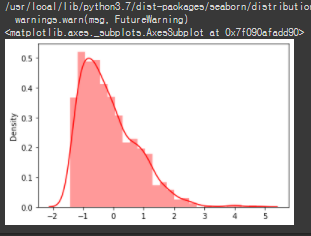
8. 정리하며...
오늘 포스팅과 유튜브 영상에서는 Box-Cox 변환이 어떤 변환인지 이해하고 Skew가 어떻게 변하는지도 같이 이해하는 공부를 해보았습니다. Lambda에 따라서 Positive Skew가 될 수 도 있고, Negative Skew가 될 수 도 있습니다. 파이썬 명령어에서 boxcox 명령어는 가장 정규분포에 가깝도록 하는 lambda를 찾아서 계산해주는 명령어입니다. 이론적으로 Optimal lambda를 어떻게 찾을 것인가는 따로 추후에 정리하도록 하겠습니다. 먼저 어떻게 찾을 것인가보다는 결과적으로 어떻게 변할 것인가에 초점을 맞추고 준비했습니다.
'빅데이터 > 통계노트' 카테고리의 다른 글
| Log Transformation 로그/지수/제곱/루트/역수 함수변환 [빅공남! 통계 같이해요] (3) | 2022.03.26 |
|---|---|
| 구간화(Binning) 더미변수(Dummy Variable) pd.cut[빅공남! 통계 같이해요] (0) | 2022.03.09 |
| MinMax Standard Robust Scaler 변수 변환 [빅공남! 통계 같이해요] (0) | 2022.03.08 |
| 파생변수 요약변수 Derived Variable Summary Variable [빅공남! 통계 같이해요] (0) | 2022.03.01 |
| SVD Singular Value Decomposition 특이값분해 [빅공남! 통계 같이해요] (1) | 2022.02.24 |




댓글