SVD Singular Value Decomposition 특이값분해 [빅공남! 통계 같이해요]

SVD Singular Value Decomposition 특이값 분해 차원축소 기법 공부 주제로 오늘 포스팅을 준비하였습니다. 오늘 내용은 행렬과 관련된 주제로 선형대수학과 관련이 깊습니다. 선형대수학에서 등장하는 행렬의 SVD 기법을 활용해서 데이터 분석에서는 어떻게 차원축소로 연결되는지 알아보고자 합니다.
1. Data는 벡터? Data는 행렬?
데이터는 각각의 행에 대해서 벡터로 볼 수 있습니다. 아개 그림과 같이 1개의 행은 1개의 Sample로 볼 수 있습니다. Sample 여러 개를 모아놓은 데이터는 행렬(Matrix)로 이해할 수 있습니다. 그래서 데이터 분석 차원에서 SVD는 데이터를 행렬(Matrix)로 보고, Matrix의 Feature를 어떻게 추출할 것인가?와 관련이 있습니다.

SVD의 아이디어는 이러한 행렬(Matrix)를 어떻게 분해할 것인가? 와 관련이 있습니다.
2. 고유값(Eigenvalue) vs 특이값(Singular Value)?
고유값(Eigenvalue), 특이값(Singular Value)는 모두 행렬에서 등장하는 개념입니다. 고유값, 고유벡터, 특이값, 특이벡터로 연결이 되는데, 일단 고유값과 특이값의 개념에 대해서 살펴보도록 하겠습니다.
1) 고유값 : 정사각행렬(nxn)에서 대각성분이 숫자이고 나머지 성분은 0인 행렬
2) 특이값 : 직사각행렬(mxn)에서 대각성분이 숫자이고 나머지 성분은 0인 행렬
아래 그림과 같이 행렬에서 대각행렬이 숫자이고 나머지가 0인 행렬을 고유값, 특이값이라고 합니다. 특이값은 특히 정사각행렬이 아니어도 가능합니다. Singular Value는 아래 그림에서 1,4,-3을 의미합니다.

3. SVD(Singular Value Decomposition)
SVD는 말 그대로 Singular Value를 가지는 행렬로 분해하는 것을 의미합니다. 아래 그림과 같이 mxn 행렬 A에 대해서 다음과 같이 그림을 분해할 수 있습니다.

그림을 보면 행렬 A = USV^t 행렬의 곱으로 분해가 가능하나는 것을 알 수 있습니다. 여기서 S는 Singular Value를 가지는 행렬을 의미합니다. 즉 대각성분만 숫자이고 나머지는 모두 0인 행렬을 의미합니다. U,V는 직교행렬(Orthogonal Matrix)를 나타내고 UU^t = I, VV^t = I 가 나오게 됩니다. 행렬 A를 SVD한다는 것의 의미는 USV^t 곱셈 형태의 행렬로 변환한다는 것을 의미하게 됩니다.
수학적인 의미를 좀더 해석해 보면
A = m x n 행렬
A = USV^t로 가정합니다. 그리고 AA^T 행렬 곱을 계산해봅니다.
A^t는 전치행렬로 행과 열을 바꾼행렬을 의미하는데
A = mxn행렬이면 A^t = nxm 행렬이 됩니다.
AA^t = (mxn)행렬 x (nxm)행렬 이므로 mxm인 정사각행렬이 등장합니다.
AA^t = (USV^t)(USV^t)^t
= (USV^t)(VS^tU^t)
= (US)(V^tV)S^tU^t
= USS^tU^t
= U(SS^t)U^t
여기서 중요한 점은 AA^t 행렬을 계산하면, 대각행렬의 고유값(Eigenvalue)로 문제로 변환해서 풀 수 있게 됩니다.
Singular Value를 가지는 행렬 S에 대해서 SS^t = Singularvalue^2을 대각성분으로 가지는 정사각행렬이 됩니다.
그래서 AA^t의 고유값(Eigenvalue)를 계산하고 이값의 루트를 붙이면 특이행렬의 Singular Value가 되는 것입니다.
이번에는 A^tA를 계산해보고자 합니다.
A^tA = (USV^t)^t (USV^t)
= (VS^tU^t)(USV^t)
= (VS)(U^tU)S^tV^t
= VS^tSV^t
= V(S^tS)V^t
마찬가지로 A^t A를 계산해도 S^tS를 대각성분으로 가지는 고유값(Eigenvalue)문제로 이해할 수 있습니다.
4. SVD의 직관적인 의미
SVD 행렬을 분해한다는 것은 어떤 의미일까? 위키피디아의 아래 그림을 보면서 직관적인 의미를 얻고자 합니다.

행렬을 SVD로 분해하면 직교행렬, Singular Value를 가지는 행렬의 곱들로 분해가 됩니다. 각각의 행렬을 좌표에서 어떤 의미인지 알아보겠습니다. 위키피디아에 그림이 잘 설명이 되어 있습니다.
행렬 M을 곱한다는 의미는 V^t만큼 회전하고, S만큼 늘리고 줄이고, 다시 U로 회전하는 것으로 이해할 수 있다는 것이 중요한 설명입니다. 아래 그림을 보면 먼저 V^t는 축(Axis)의 회전을 나타내고, S는 분포의 늘리고 줄이고를 나타내며, U는 회전인 것을 눈으로 쉽게 볼 수 있습니다.
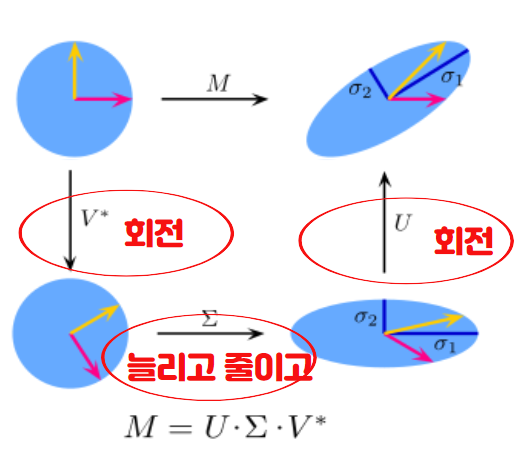
아래 그림처럼 mxn 행렬 A는 SVD로 분해과 되고 결국 가운데 Singular Value는 벡터를 늘리고 줄이는 것과 연관이 됩니다. 이처럼 데이터를 늘리고 줄이는 부분은 데이터의 분산과 연관이 됩니다. 얼마나 멀리 퍼져있는가 즉, 얼마나 늘리고 줄이는가와 연관이 되는 것입니다.

5. SVD와 차원축소와는 무슨 상관??
아래 그림처럼 데이터 Set A는 행렬 A로 볼 수 있습니다. 이 행렬을 SVD로 USV^t로 분해해서 보겠다는 것은 아래 그림과 같이 이해해 볼 수 있습니다.
A : Data Set ☞ Matrix
V : Data Sample Length in Data Set on V
S : magnitude of directions (늘리고, 줄이고 분산과 연관)
V^t : direction of greates variance (분산을 나타내는 방향)
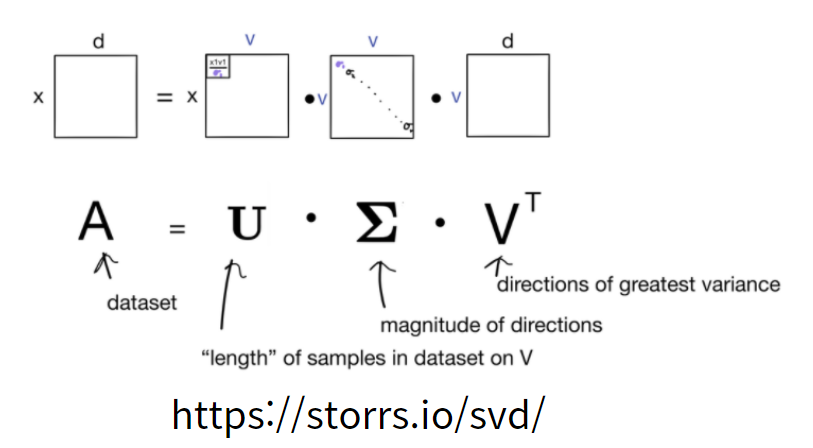
중요한 점은 Singular Value를 가지는 행렬은 데이터의 분산의 정도를 나타내며, V는 분산을 나타내는 방향을 나타내게 됩니다. 차원을 축소하겠다는 의미는 이중 일부의 분산을 가지고 데이터 전체를 표현하겠다는 것을 의미합니다. 이러한 개념은 Full SVD, Truncated SVD로 연결됩니다.
6. Full SVD, Truncated SVD
차원축소 개념은 결국 Truncated SVD를 의미합니다. Full SVD는 행렬을 분해하는 것을 의미하고, Truncated SVD는 FUll SVD에서 일부의 기저로 데이터를 보현하는 것을 의미합니다. 아래와 같이 정리해보았습니다.
1) FUll SVD : 수학적 개념의 SVD, 즉, 행렬을 USV^t로 분해하는 것을 의미함.
2) Truncated SVD : Full SVD에서 일부이 기저(Basis)로 행렬을 나타냄.
직관적인 의미를 돕기 위해서 아래 그림으로 이해해보고자합니다. 그림의 윗부분은 Full SVD를 의미합니다. 말 그대로 수학적인 의미로 행렬을 분해한 것을 의미합니다. 그림의 아랫부분은 Truncated SVD를 의미합니다. Full SVD 행렬에서 U,V를 일부 k개의 벡터만 선택해서 Ak로 나타냅니다. 이때 U,V를 각각 k개 선택하게 되면, Singular Value의 대각성분도 k개만 선택하게 됩니다.

앞선 4번 설명에서 SVD의 직관적인 의미는 U,V는 회전과 관련된 행렬이고, S는 늘리고, 줄이고 즉 분산과 연결된다고 했었습니다. 차원축소를 한다는 의미는 분산의 일부정보로 차원을 줄여서 원본 데이터를 보겠다는 의미입니다. 그래서 Singular Value 값의 큰 순서대로 일부만 택해서 k차원의 Ak를 만들어 내게 됩니다. 복잡한 차원의 A를 k차원의 Ak로 축소해서 보는 것입니다.
7. Full SVD 파이썬 코딩 실습
이번에는 구글 코랩에서 파이썬 코딩 실습으로 Full SVD를 해보고자합니다. numpy의 linear algebra(선형대수) 관련 모듈로 행렬을 분해할 수 있습니다. 다음 과 같이 행렬을 random하게 만들어 낼 수 있습니다.
import numpy as np
matrix = np.random.random((6, 3)).round(1)
matrix
이제 행렬을 SVD로 분해해보고자 합니다. from numpy.linalg import svd를 통해서 할 수 있습니다.
SVD는 3개의 행렬로 분해가 되기 때문에 변수로 3개를 얻어와야 합니다.
from numpy.linalg import svd
U, S, VT = svd(matrix, full_matrices=True)
U.shape, S.shape, VT.shape,
위의 코딩 결과를 보면 (6x6), (3x1) (3x3)행렬로 행렬이 분해된 것을 알 수 있습니다. 이제는 이 행렬을 표현해보겠습니다.
U.round(1), S.round(1),VT.round(1)
위의 결과 처럼 3개의 행렬로 분해 된 것을 알 수 있습니다. 여기서 가운데 S는 Singular Value만 표시된 행렬로 표현됩니다. 3개의 Singular Value를 가지기 때문에 3개의 행벡터 처럼 결과가 나왔습니다. 이처럼 파이썬에서 numpy로 행렬을 SVD로 분해하는 것을 해보았습니다. 수학적인 계산으로 행렬을 분해한 것이고 Full SVD를 한 것입니다.
8. Truncated SVD 활용 차원축소 (싸이킷런 이용)
이번에는 싸이킷 런을 활용해서 Data 분석에서 어떻게 차원축소가 되는지 알아보고자 합니다. 아래 그림처럼
from sklearn.decomposition import TruncatedSVD 명령어를 통해서 차원을 축소해보고자합니다.
싸이킷런의 데이터 셋명령어로 iris 데이터 샘플을 가지고 왔습니다. 중요한 점은 아래 부분입니다.
TruncatedSVD(n_components=2)는 2차원으로 데이터 차원을 축소하겠다는 것을 나타냅니다.
fit_transform(data)는 데이터를 2차원 Truncated SVD로 변환하겠다는 것을 나타냅니다.
1) Sklearn Truncated SVD로 2차원 차원축소 파이썬 코딩예제
from sklearn.decomposition import TruncatedSVD
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
data=load_iris().data
target=load_iris().target
target_names = load_iris().target_names
#SVD로 2차원 차원축소
trunc_SVD = TruncatedSVD(n_components=2)
data_TSVD = trunc_SVD.fit_transform(data)for c, i, target_name in zip(["orange","pink","blue"], [0, 1, 2], target_names):
plt.scatter(data_TSVD[target == i, 0], data_TSVD[target == i, 1], c=c,edgecolors='black', label=target_name)
plt.legend()
plt.title('Truncated SVD Result')
plt.xlabel('SVD axis1')
plt.ylabel('SVD Axis2')위의 코딩을 통해서 2차원으로 차원을 축소하면 아래와 같은 결과를 얻어 낼 수 있습니다.

차원축소 기법 중에 하나인 SVD를 이해하기 위해서 열심히 포스팅을 준비했습니다. 직관적인 의미를 이해하고 간단한 파이썬 코딩을 통해서 어떻게 차원축소를 해서 보는지도 이해하도록 정리를 해보았습니다. 유튜브 영상에서 SVD에 대해서 설명을 하고자 만들어보았습니다. 빅공남 유튜브 채널 구독과 좋아요는 빅공남을 힘나게 합니다.
'빅데이터 > 통계노트' 카테고리의 다른 글
| MinMax Standard Robust Scaler 변수 변환 [빅공남! 통계 같이해요] (0) | 2022.03.08 |
|---|---|
| 파생변수 요약변수 Derived Variable Summary Variable [빅공남! 통계 같이해요] (0) | 2022.03.01 |
| LDA Linear Discriminant Analysis [빅공남! 통계 같이해요] (0) | 2022.02.14 |
| Scree Plot PCA Eigenvalue Explained Ratio [빅공남! 통계 같이해요 ] (0) | 2022.02.09 |
| PCA Principle Component Analysis 주성분분석 [빅공남! 통계 같이해요] (0) | 2022.02.05 |




댓글